Gizli Duvarlar
En az enerji harcama yasası doğanın en çok bilinen yasalarından biridir.
Örneğin, A noktasından yayılan ışık B noktasına gitmek için sonsuz tane yol arasından en çabuk gidebileceği yolu seçer. Eğer A ve B noktaları havadaysa, ışık AB doğrusunu izler, çünkü AB doğrusu ışığın hedefine en çabuk varacağı, en az enerji harcayacağı yoldur.
Eğer A noktası havada, B noktası sudaysa, ışık A’dan B’ye gitmek için kırılır çünkü ışık havada daha hızlı gider, suda yavaşlar, dolayısıyla olabildiğince havada kalmak ister. Doğanın bu yasasına fizikte sık sık rastlanır.
Estetik bilincimiz doğadan ve doğa yasalarından kaynaklanır. Doğanın en az enerji harcama yasası estetikte de geçerlidir. Güzelliği çoğu zaman yalında buluruz. Yazında olsun, resimde olsun, mimaride olsun, matematikte olsun, nerede olursa olsun gereksiz karmaşadan hoşlanmam, hep yalından yanayımdır. Yazında örneğin, eğer bir tümce bir düşünceyi, duyguyu, olayı, durumu anlatmaya yetiyorsa, ikincisine gerek yoksa o gereksiz ikinci tümceyi okumamalıyım. Gereksiz uzun tümcelerden de hoşlanmam. Bir tek sözcük, yerinde kullanılmışsa ve iyi seçilmişse, koca bir sayfanın işlevini görebilir. İşte bir yazın yapıtında o sözcüğü bulmak isterim.
Resimde de öyle. Gereksiz çizgiden, gereksiz renkten rahatsız olurum. Sanatçıdan düşüncesini, görüşünü, duygusunu en az enerjiyle anlatmasını beklerim. Örneğin Giacometti’nin çok çizgili eskiz–resimlerine bayılırım, çünkü çizgileri ne kadar gerekiyorsa onca çoktur, bana göre bir tek fazla çizgi yoktur Giacometti’de.
Yalına ve güzelliğe ulaşmak hiç de kolay değildir. Kolay olsaydı herkes sanatçı olabilirdi. Picasso’nun bir dizi boğa taşbaskısı vardır. Ardarda, bir iki gün içinde yapılmıştır. İlk taşbaskıda bütün ayrıntılarıyla oldukça gerçekçi bir boğa görürüz. İkinci taşbaskıda daha az ayrıntı vardır. Son taşbaskıda üç beş çizgi kalmıştır salt. Bu son taşbaskı öylesine yalındır ki, Evren Paşa gibi, “Bunu ben de yaparım,” dedirtir insana.
Aslında ben Evren Paşa’yı çok iyi anlıyorum, hatta hak veriyorum ve çocuksu bir saflıkla söylediği bu sözlerde, başka hiçbir söylevinde göremediğim bir gerçek görüyorum. Tek kusuru, bu sözleri 60 küsur yaşlarında söylemesidir.
Beğendiğimiz modern sanat müzelerinden, “Bunları ben de yapabilirim,” duygusuyla çıkmaz mıyız? Bilimsel bir kitabı iyi anlamışsak, yazarın düşüncesini iyi kavramışsak ve yazara hak veriyorsak, o buluşları –isteseydik, zamanımız olsaydı ve doğru çağda yaşasaydık– biz de bulabilirmişiz gibi bir duyguya kapılmaz mıyız?
Matematikçi bir arkadaşım, bir kahvede sohbet ederken, bütün ciddiyetiyle, “Geçen yüzyıl yaşasaydım, amma teorem kanıtlardım ha!” demişti bir gün.
Freud’un, Darwin’in, Marx’ın buluşları bugünün insanına yalın gelir, “Bunları ben de bulabilirdim” dedirtir. Doğrudur. Gerçek yalındır. Ama o yalın gerçeğe ilk ulaşmak öylesine zordur ki…
Picasso yılların deneyimiyle ve kuşku götürmez dehasıyla bir iki gün içinde yalına ulaşabilir. Biz ölümlülerse yalına ulaşmak için çok çalışmalıyız. “En az enerjiye” ulaşmak için çok enerji harcamalıyız. Aşağıda buna güzel bir örnek bulacaksınız.
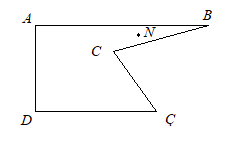
Aşağıdaki şekle bir göz atın. Bu ABCÇD beşgenini bir oda olarak düşünün. Beş kenarlı tuhaf bir oda… Bu odanın bir başka tuhaflığı daha var. Odanın içindeki N noktasından bakıldığı zaman, CÇ ve ÇD duvarları görünmüyor, ayrıca AD duvarının bir bölümü saklı, yalnızca bir bölümü görünüyor. Öte yandan AB ve BC duvarları tümüyle görünüyor.
Birinci Soru. Öyle bir köşegen oda çizin ki ve bu odanın öyle bir noktası olsun ki, bu noktadan bakıldığında, odanın hiçbir duvarı tamamıyla görünmesin. (Kimi duvarlar hiç görünmeyebilir.)
İkinci Soru. Eğer yukarda bulduğunuz köşegen odanın altıdan fazla duvarı varsa, size bir sorum daha var. Öyle bir altıgen oda çizin ki ve bu altıgen odanın içinde öyle bir nokta olsun ki, bu noktadan bakıldığında altı duvarın hiçbiri tamamıyla görünmesin.
Birinci Sorunun Yanıtı: Herkesin ayrı bir yanıtı olabilir. Ben bulduğum ilk köşegeni göstereyim. Önce, her kenarı 6 birim uzunluğunda bir kare çizelim:
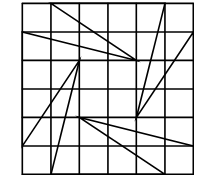
Oradan bakıldığında, hiçbir duvarın tam olarak görülemeyeceği nokta bu karenin merkezi olacak. Odanın duvarları daha belli değil. Yukarıdaki kareyi yontmamız gerekecek. Aşağıdaki çizgileri çizelim.
Şimdi, bu son çizdiğimiz çizgilerden kareyi keselim. Aşağıdaki şekli elde ederiz:
İşte odamız. On iki duvarlı. İşe başladığımız karenin merkezinden bakıldığında hiçbir duvar tam olarak görünmez.
Yukardaki odanın duvar sayısını azaltabilir miyiz? Evet. Dikkat ederseniz, yatay ve dikey duvarlar pek gerekli değil. Yukardaki odanın sekiz duvarını yıkıp yerine dört yeni duvar öreceğiz, böylece duvar sayımız azalacak. Önce aşağıdaki çizgileri çekelim:
Şimdi bu çizdiğimiz çizgilerden odamızı keselim:
İşte yeni odamız. Merkezden bakarsak yine hiçbir duvarı tam olarak göremeyiz. Bu kez odamızın sekiz duvarı var.
Sıra ikinci soruya geldi.
İkinci Sorunun Yanıtı: Yukarıda kareyle yaptığımızı bir üçgenle yapacağız ve sekiz duvarlı yerine altı duvarlı bir oda elde edeceğiz.
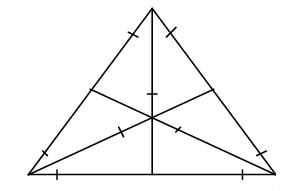
İlk önce, açıortaylarıyla birlikte bir eşkenar üçgen çizelim ve bu üçgenin üstünde aşağıdaki gibi 9 nokta belirleyelim.
Odamızın merkezi üçgenin merkezi olacak. Odanın duvarlarını daha belirlemedik. Bu üçgeni biraz yontacağız.
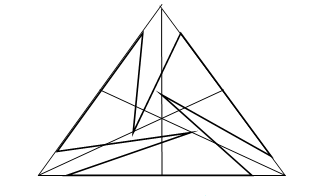
İkinci iş olarak, bu noktalardan birkaçını aşağıdaki gibi doğrularla birleştirelim.
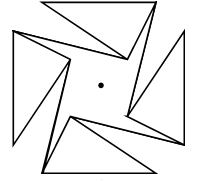
Bu son çizdiğimiz doğrulardan üçgenimizi keselim.
Bu odanın merkezinden bakıldığı zaman hiçbir duvar tam olarak görülmez. Ama odanın dokuz duvarı var. Duvar sayısını azaltabilir miyiz? Evet. Altı duvarı silip yerine üç duvar çıkabiliriz. Önce odaya aşağıdaki çizgileri çekelim:
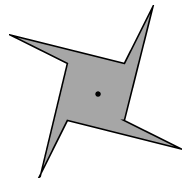
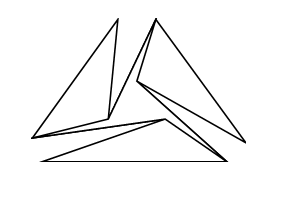
Şimdi de gereksiz üç üçgeni atalım.
İşte odamız. Altı duvarlı ve merkezden bakıldığında hiçbir duvar tam olarak görünmüyor.
Yazar: Ali Nesin (tümünü gör)
- Matematik ve Doğa - 18 Aralık 2019
- Loto! - 25 Eylül 2019
- Cemal Amca’nın Zarları - 29 Ağustos 2019
- Şapka Problemi - 15 Ağustos 2019
- Çok Basit Aritmetiğe Çok Basit Bir Çözüm - 1 Ağustos 2019