Bouncing Cubes and π (3Blue1Brown)
Yesterday, I have noticed the wonderful video by 3Blue1Brown regarding bouncing cubes and the number \(\pi\). Here is the video, please watch it. The answer to the problem will be given on January 20th, 2019:
The problem can be stated as follows:
“You have two masses on a frictionless surface, where one mass is \(10^N\) times heavier than the lighter one. Initially the small mass \(m\) has no velocity and bigger mass \(M = 10^N m\) is pushed towards the lighter mass. The small mass \(m\) is between a wall and the heavy mass \(M\). Find the number of collisions between two masses. Collisions between masses and the wall are assumed to be perfectly elastic, that is no energy is lost during one collision.”
I will give a spoiler (actualy 3Blue1Brown already gave the answer): The number of collisions is proportional to \(\pi 10^{N/2} = \pi \sqrt{10^N}\)! This marvelous fact was alone enough to divert all my attention to investigate, why?
Let’s start from two billiard balls, one is moving towards the other. If the masses are the same, all momentum of the moving ball is transferred to the other ball:

If the moving ball is heavier than the stationary ball, small ball will move with higher velocity and both will move in the same direction:

If the moving ball is lighter than the stationary ball, lighter ball will move in the opposite way with lower speed.

Think of this: If Shaquille O’Neal rams you, you will get pushed away with higher velocity. If you do the same to Shaq, not much will happen to that big guy. Put a tennis ball on a basketball. Drop both of the balls while tennis ball is on top of the basketball, tennis ball will fly around.
OK, going back to our problem… Imagine our heavy ball \(M\) and small ball \(m\) are moving to the right with velocities \(v\) and \(u\), respectively. \(v\) is greater than \(u\), so at some point \(M\) will catch \(m\) and hit it. Let \(v’\) be the velocity of \(M\) and \(u’\) be the velocity of \(m\) after collision.


Due to momentum conservation, we have the equation:
\(p_{initial} = p_{final}\)
\(mu + Mv = Mv’ + mu’\)
But the collision is elastic, so we also have energy conservation equation:
\(E_{initial} = E_{final}\)
\(\frac{1}{2} m u^2 + \frac{1}{2}M v^2 = \frac{1}{2}m (u’)^2 + \frac{1}{2}M (v’)^2\)
By solving for \(v’\) and \(u’\), I have found the following equations:
\(v’ = \left(\frac{2m}{M+m}\right) u+\left(\frac{M-m}{M+m}\right)v\)
\(u’ = \left(\frac{m-M}{m+M}\right) u + \left(\frac{2M}{M+m}\right)v\)
Now define a new variable \(\alpha = m/M\) and write down the previous velocities as the following:
\(v’ = \left(\frac{2 \alpha}{1+\alpha}\right) u+\left(\frac{1-\alpha}{1+\alpha}\right)v\)
\(u’ = \left(\frac{\alpha-1}{1+\alpha}\right) u + \left(\frac{2}{1+\alpha}\right)v\)
This allows me to write the equations for velocities in matrix form:
\(\left(\begin{array}{c} u’\\v’ \end{array}\right) = \left(\begin{array}{cc} -\left(\frac{1-\alpha}{1+\alpha}\right) & \left(\frac{2}{1+\alpha}\right)\\ \left(\frac{2 \alpha}{1+\alpha}\right) & \left(\frac{1-\alpha}{1+\alpha}\right) \end{array}\right)\left(\begin{array}{c} u\\v \end{array}\right)\)
And for shorthand notation,
\(\left(\begin{array}{c} u’\\v’ \end{array}\right) = \mathcal{R}(\alpha)\left(\begin{array}{c} u\\v \end{array}\right)\),
where \(\mathcal{R}(\alpha)\) is obviously
\(\mathcal{R}(\alpha) = \left(\begin{array}{cc} -\left(\frac{1-\alpha}{1+\alpha}\right) & \left(\frac{2}{1+\alpha}\right)\\ \left(\frac{2 \alpha}{1+\alpha}\right) & \left(\frac{1-\alpha}{1+\alpha}\right) \end{array}\right).\)
This is the equation after they collide. That’s one “clank.” Now, \(m\) moves towards the wall and bounces back. When it bounces back, the speed stays the same, but the velocity changes sign. The velocity of the heavy ball is unaffected. If the velocities of masses \(M\) and \(m\) are \(v’\) and \(u’\), respectively, let \(v”\) and \(u”\) are the velocities after small ball bounces back from the wall. Clearly, \(v” = v’\), since heavy mass is unfazed, \(u” = -u’\), since small mass just changes direction. I can represent this case with matrix,
\(\left(\begin{array}{c} u”\\v” \end{array}\right) = \left(\begin{array}{cc}-1 & 0 \\ 0 & 1\end{array}\right)\left(\begin{array}{c} u’\\v’ \end{array}\right)\)
Again with shorthand notation,
\(\left(\begin{array}{c} u’\\v’ \end{array}\right) = \mathcal{S}\left(\begin{array}{c} u\\v \end{array}\right)\)
where
\(\mathcal{S} = \left(\begin{array}{cc}-1 & 0 \\ 0 & 1\end{array}\right).\)
The whole motion is basically one application of \(\mathcal{R}(\alpha)\) for a collision and then \(\mathcal{S}\) for reflection. Those are two “clanks.” For an arbitrary \(j\)th collision, we can find the velocities of balls \(v^{(j)}\), \(u^{(j)}\) as,
\(\left(\begin{array}{c} u^{(j)}\\v^{(j)} \end{array}\right) = \mathcal{S}\mathcal{R}(\alpha)\left(\begin{array}{c} u^{(j-2)}\\v^{(j-2)} \end{array}\right)\)
We turned the problem into the following: How many \(N\) times should we apply the matrices to the initial velocity until \(|v^{(j)}| > |u^{(j)}| \), \(j>1\)?
\(\left(\begin{array}{c} u^{(j)}\\v^{(j)} \end{array}\right) = \underbrace{\mathcal{S}\mathcal{R}(\alpha)\mathcal{S}\mathcal{R}(\alpha)…\mathcal{S}\mathcal{R}(\alpha)\mathcal{S}\mathcal{R}(\alpha)}_{N}\left(\begin{array}{c} u^{(0)}\\v^{(0)} \end{array}\right)\)
Note that the matrix product, and so the vectors, \(u^{(j)}, v^{(j)}\), are actually a definite polynomial of \(\alpha\). But I want to show how the velocities cross each other from another way. Very well. Now, remember back that we start our velocities as \(v^{(0)} = V_0\) and \(u^{(0)} = 0\). The big mass bullies the other small mass towards the wall and at some point, \(M\) changes the sign and small mass \(m\) continues to collide. This continues until when? This continues until small mass \(m\) cannot catch the big guy \(M\)! There was a reason I chose the parameter as \(\alpha = m/M\). After each collision, each of the velocities get smaller and smaller since \(\alpha = 10^{-N} < 1\).
OK, let’s test this… I will start from \(\alpha = 10^{-1}\), this means \(M = 10 m\). I will color the velocity of \(M\) with red, \(m\) with blue. \(M\) starts with some initial velocity \(V_0\) and \(u^{(0)} = 0\).
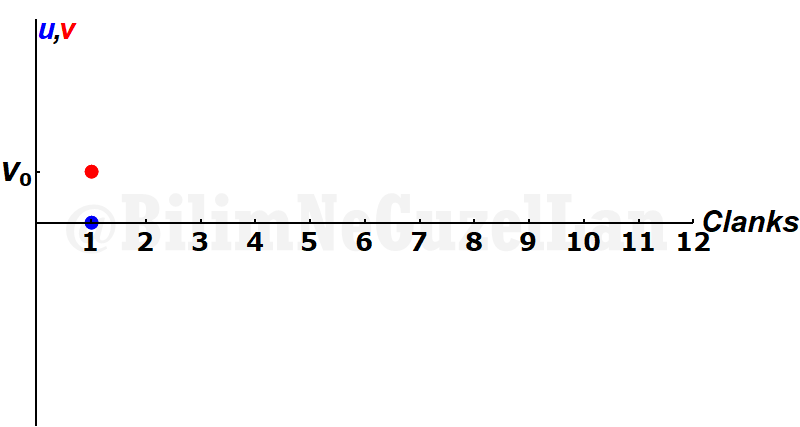
Big mass catches the small mass and pushes it…
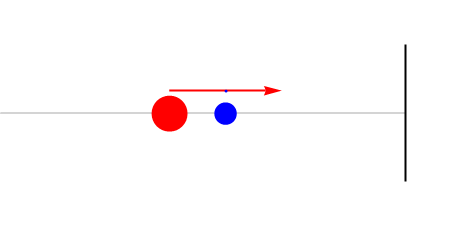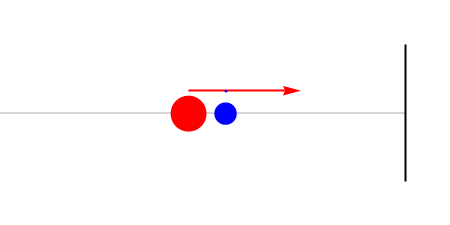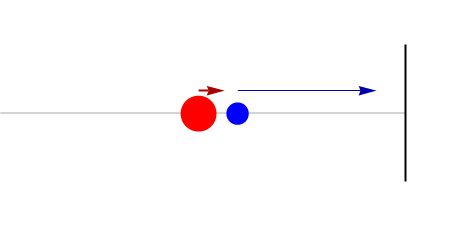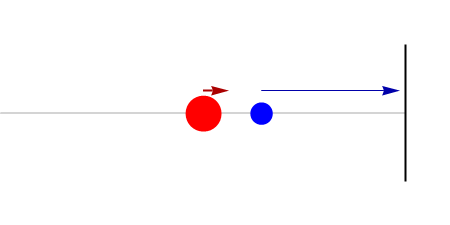
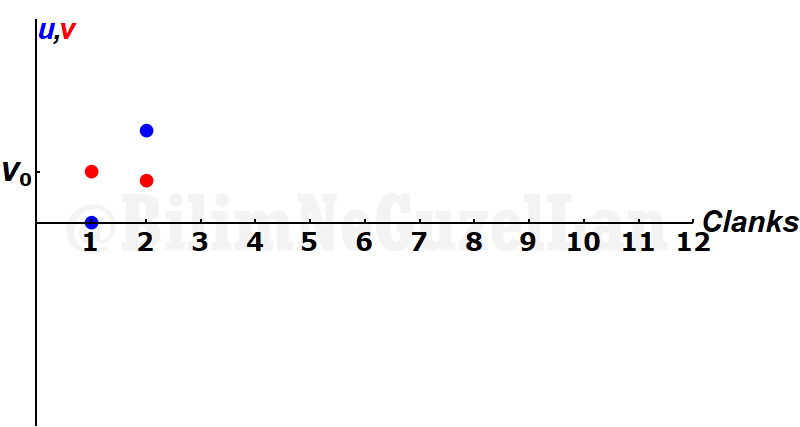
The small mass collides with the wall. Its velocity just changes sign.
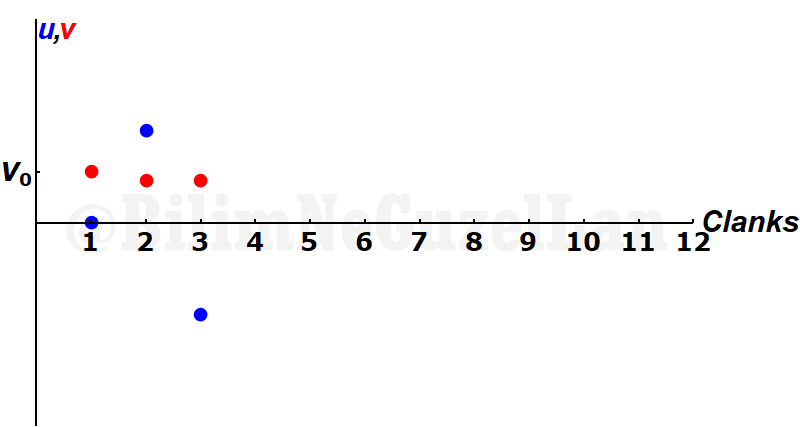
Then, returning \(m\) collides again with \(M\)…
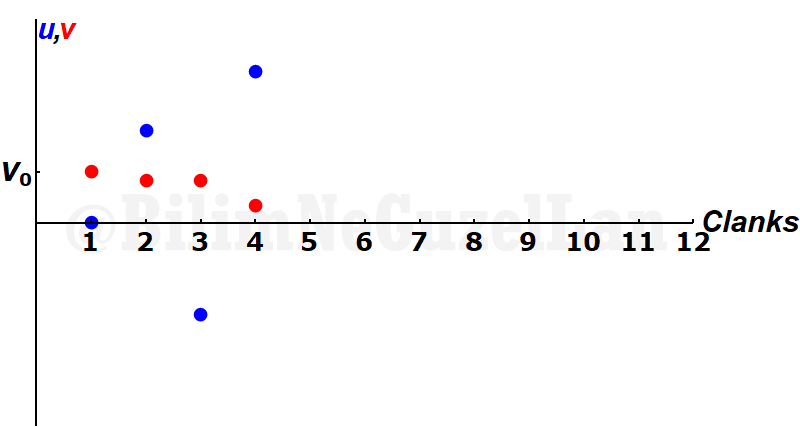
And it collides with the wall again. Its velocity changes sign…
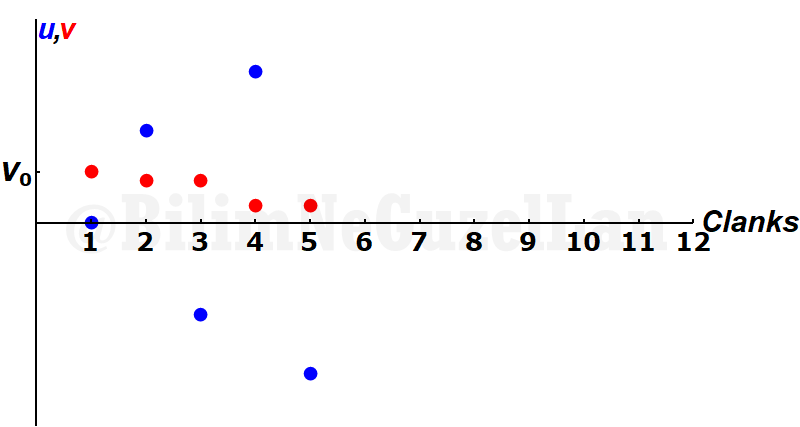
This goes on and on… At this point, big mass \(M\) changed direction.
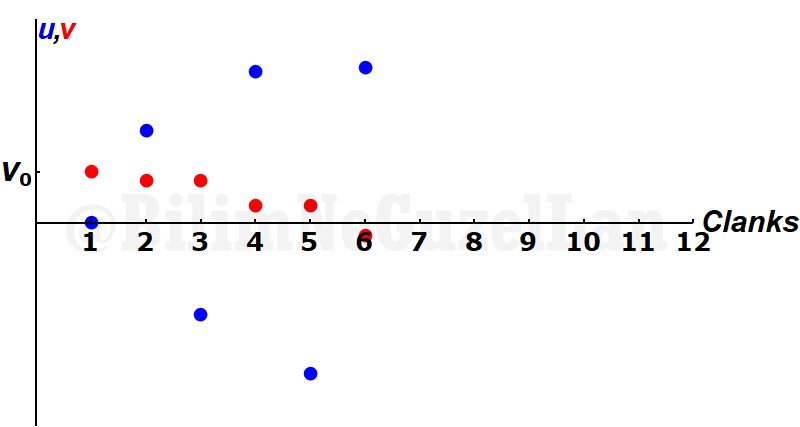
Until, the small mass cannot catch the \(M\). This means that the absolute value of the \(u\) should be smaller than \(v\), \(|u| < |v|\).
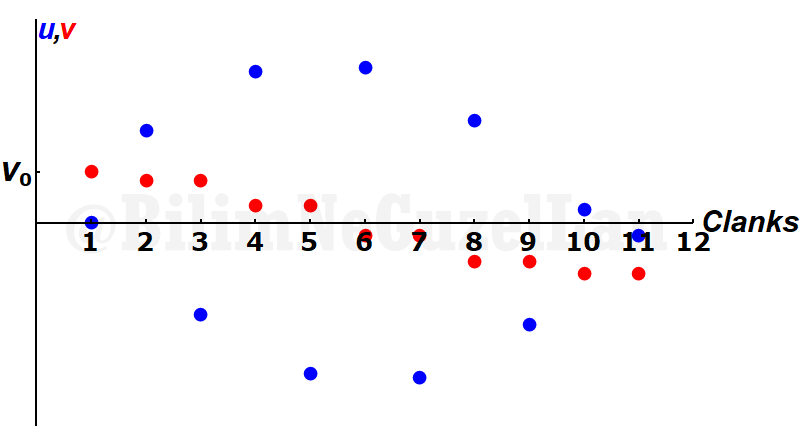
Let me take the absolute value of the velocities to see it better:
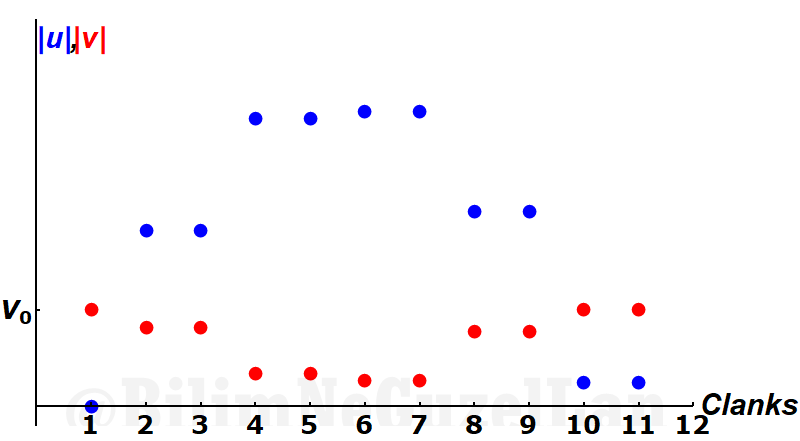
Two velocities cross each other at 9th collision. So there are 10-1 = 9 “clanks” of small mass \(m\). According to the first equation I have described above, \(M/m = 10\), ratio of number of “clanks” to the square root of \(M/m\) should be close to \(\pi\), of which it is! \(9/ \sqrt{10^1} \approx 2.84605\) the difference is, \(|\pi – 9/ \sqrt{10^1}| \approx 0.295543\), that’s \(9.4\%\) error! Not bad. If I decrease the ratio \(\alpha = m/M\) by one order of magnitude, \(\alpha = 10^{-2}\), I get this graph:
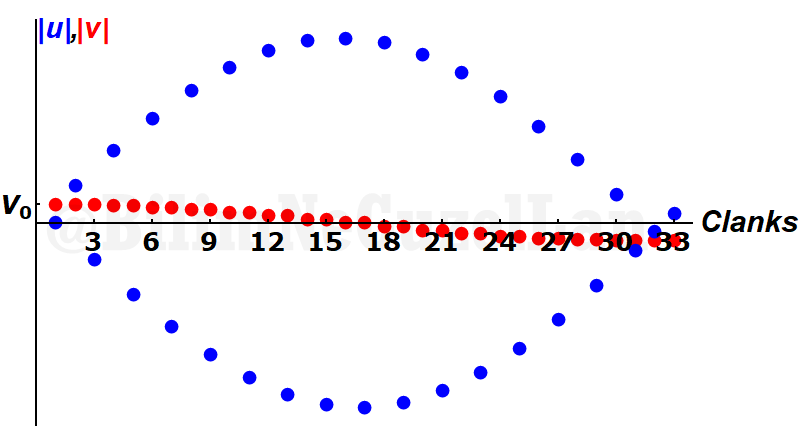
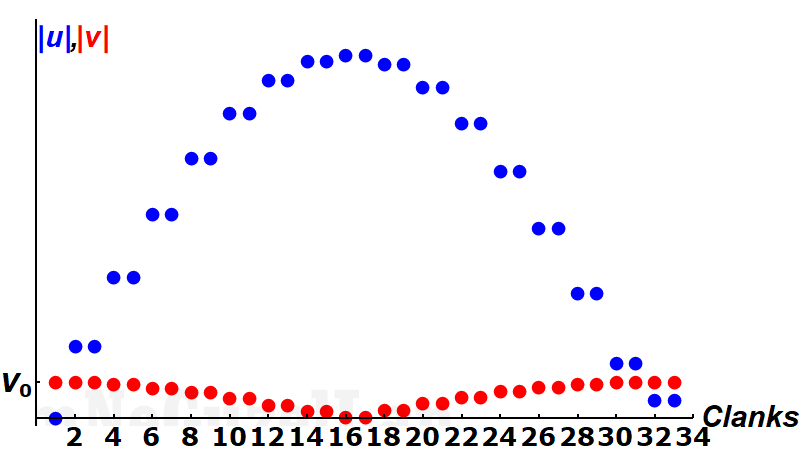
They cross each other at 31st clank. Again, \(31/\sqrt{10^2} = 3.1\). Our error is now \(1.32\%\).
I have tried also for \(\alpha = 10^{-6}\) here is the graph of the velocities:
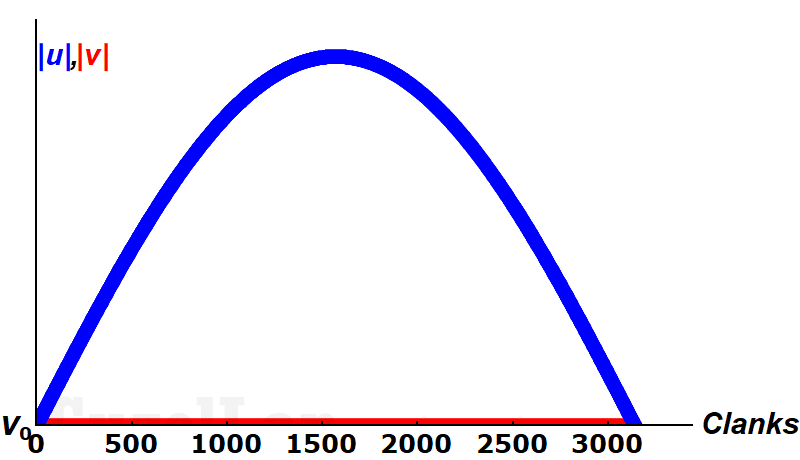
You see, velocity of the small ball gets very high compared to heavy ball, it is hard to see the velocity of the heavier ball in this graph. I will tell you when two velocities cross each other: It is 3141 clanks. \(3141/\sqrt{10^6} = 3.141\). The percentage error is \(0.013\%\). Much better!
When I tried for \(\alpha = 10^{-11}\), it clanked 993457 times, and the error is \(8.3 \times 10^{-5} \% \).
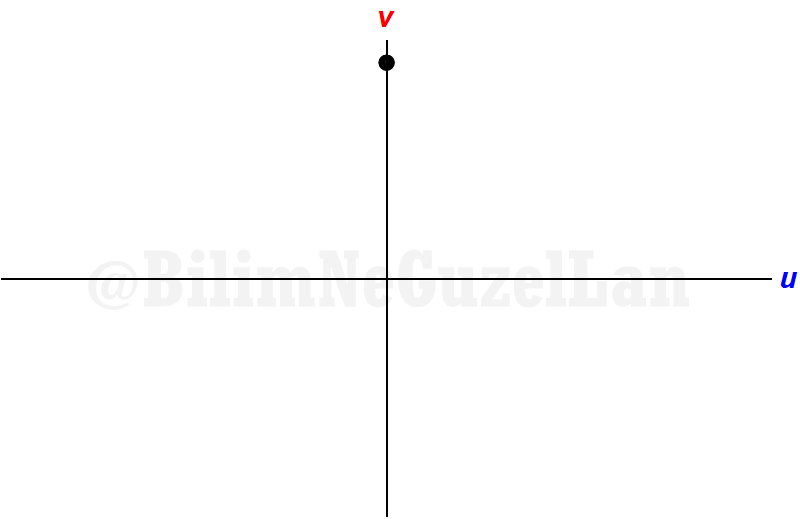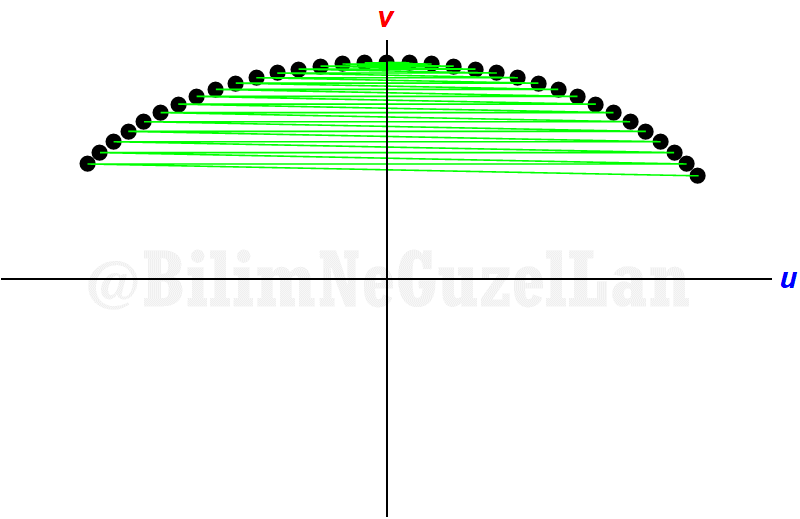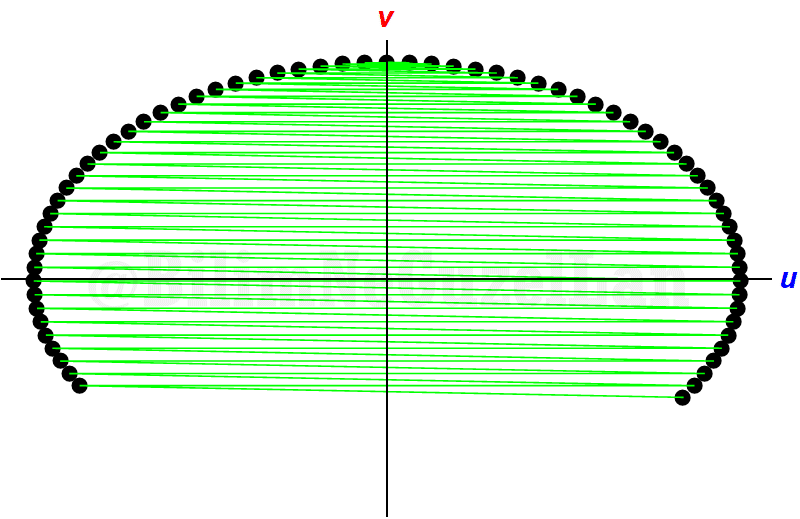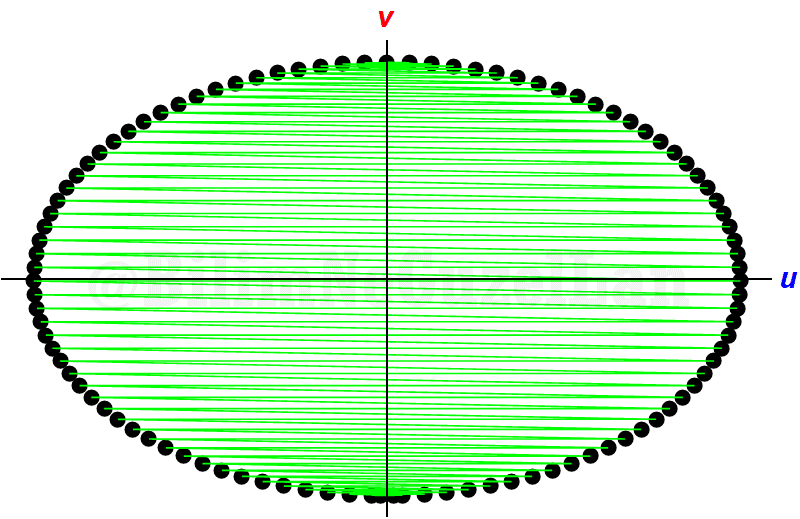
Now, why does that happen? Why is this close to \(\pi\)? You will immediately understand when I put one velocity to one axis, other velocity to other axis. This is for \(\alpha = 10^{-1}\),
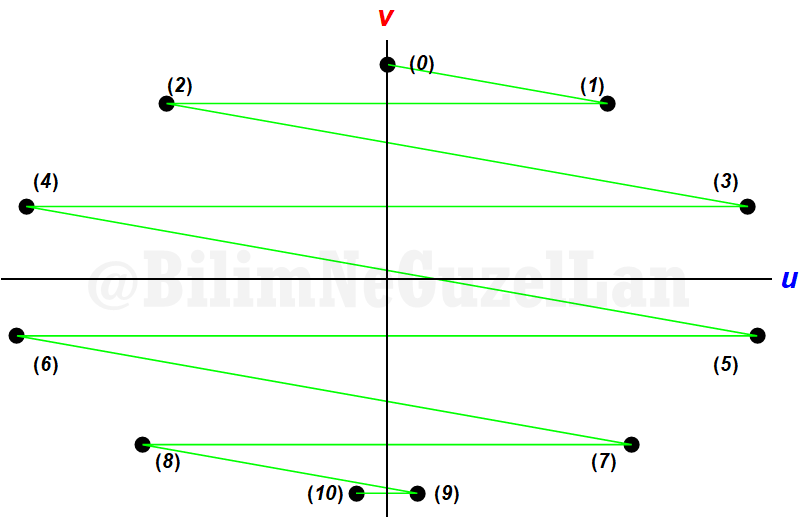
As the collisions happen, velocities look like this:
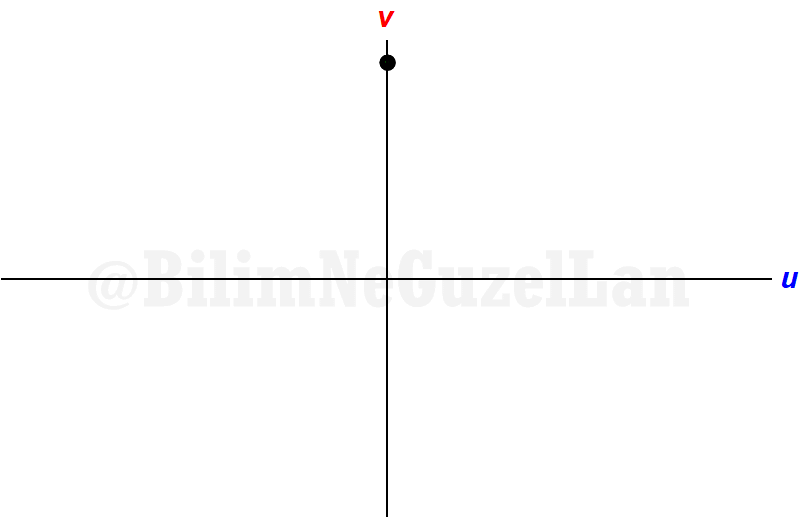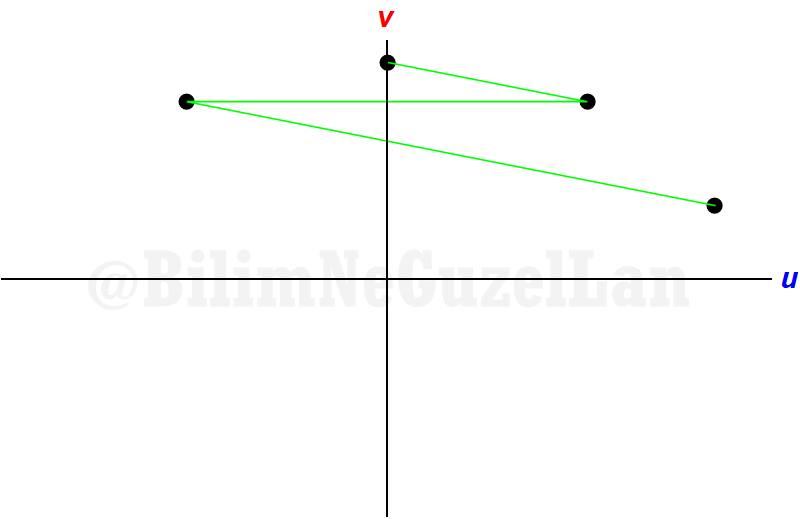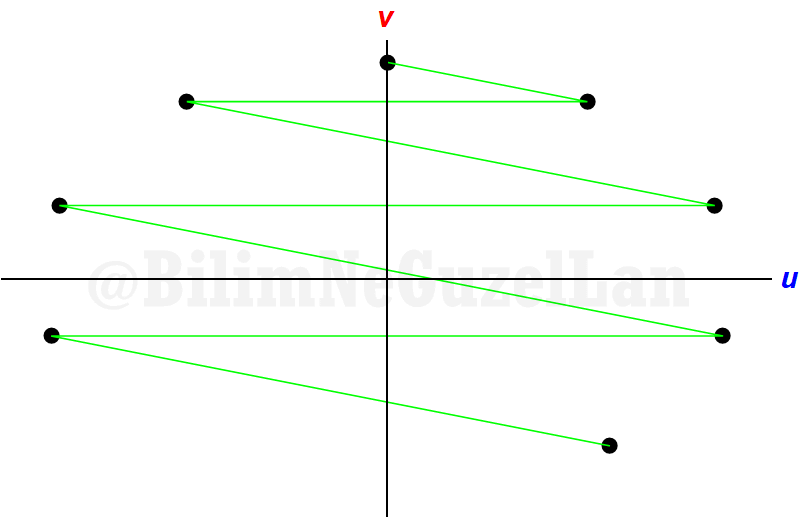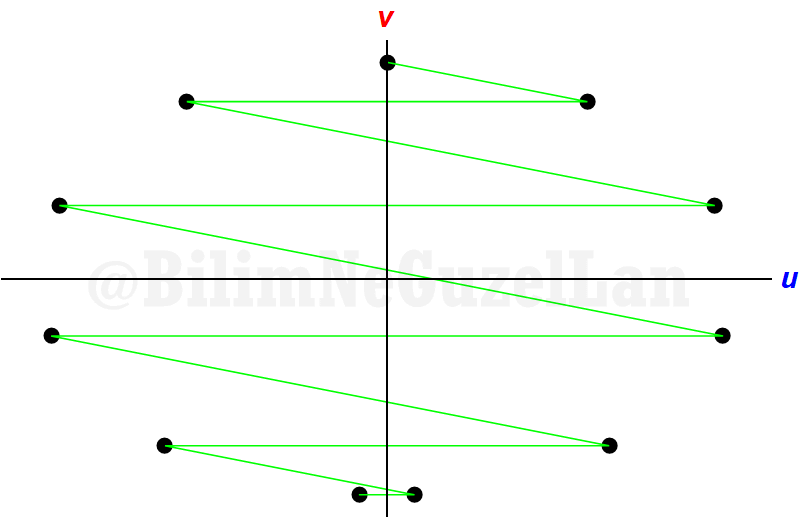
One collision, one reflection, one collision, one reflection… For \(\alpha = 10^{-2}\),
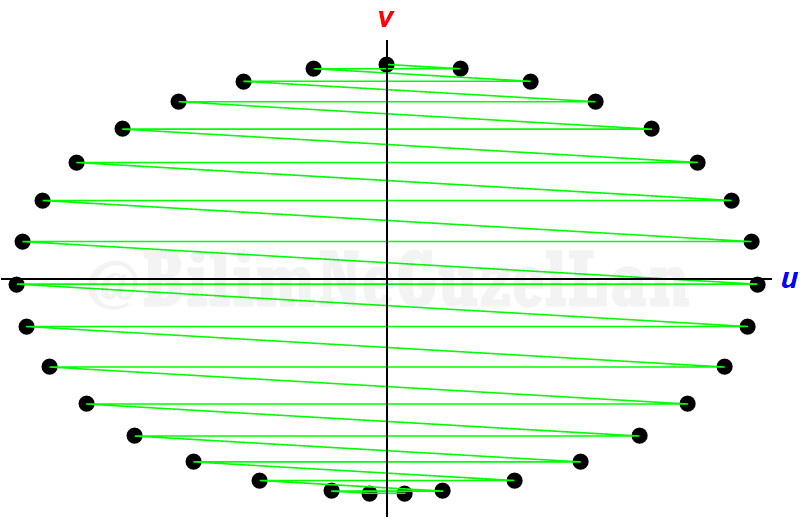
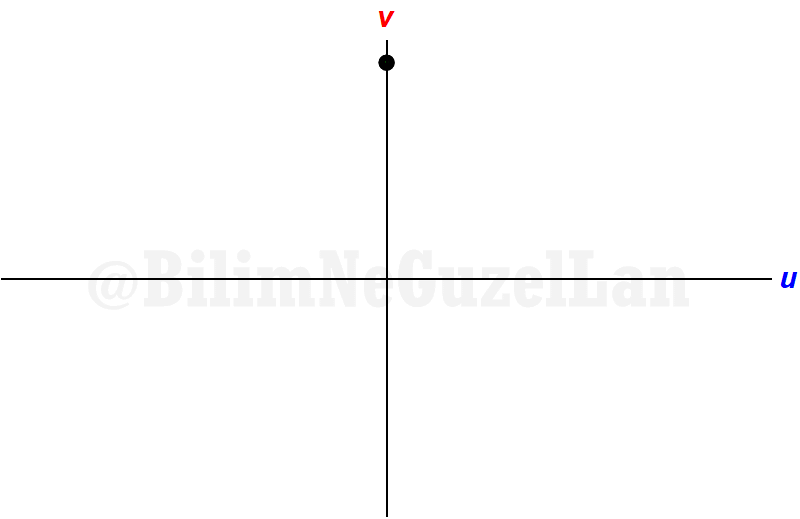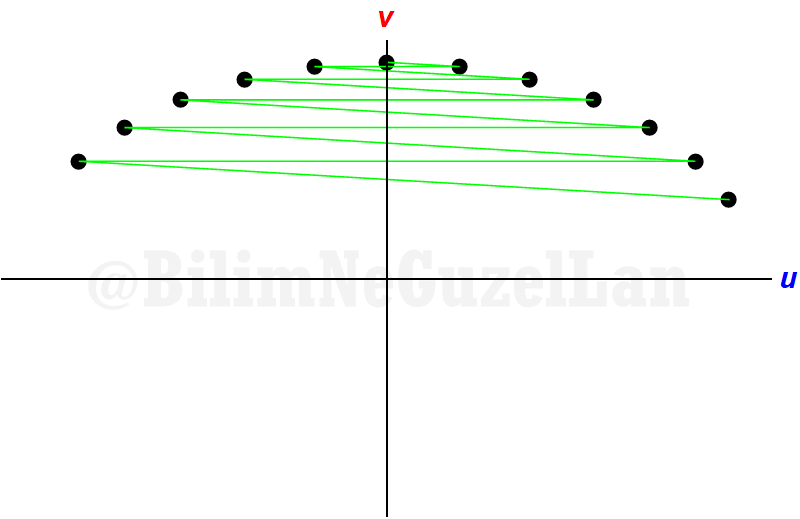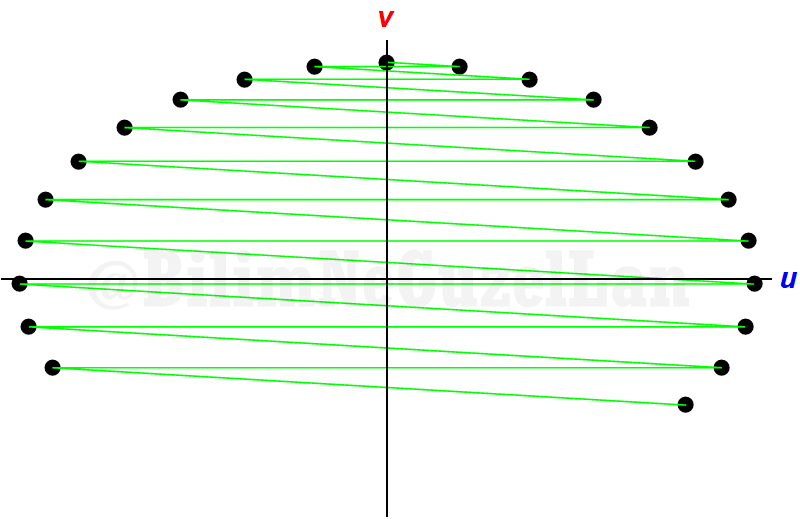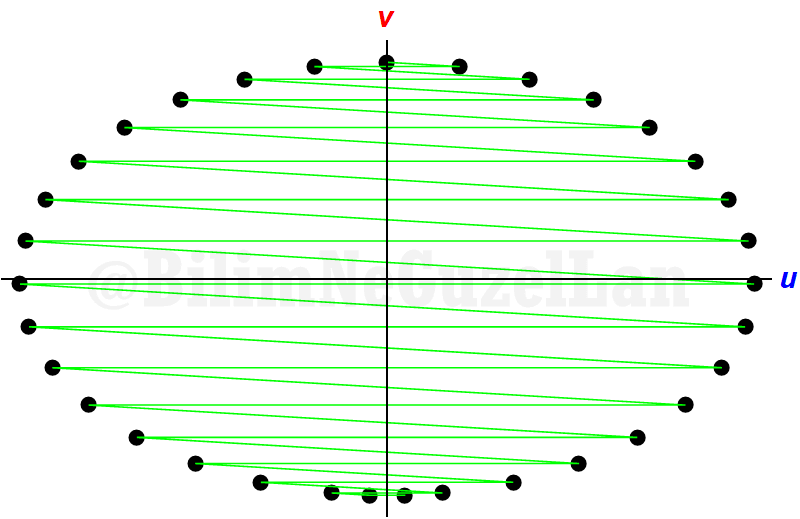
And \(\alpha = 10^{-3}\):
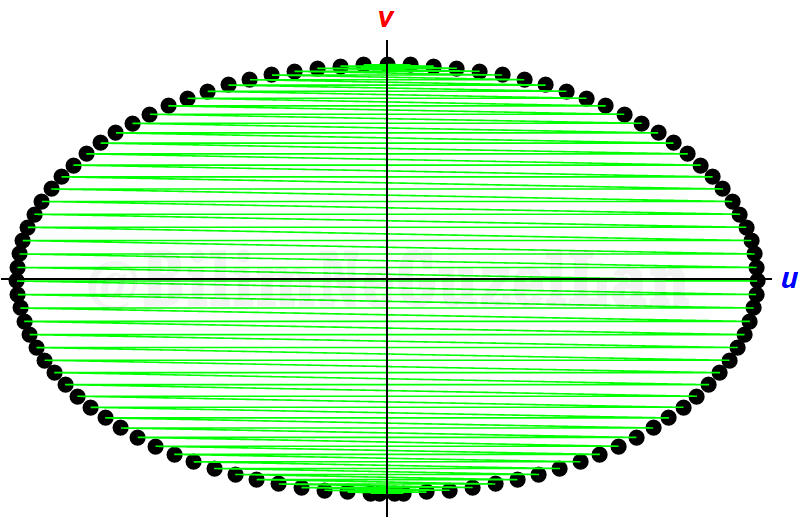
Well, this looks like an ellipse? Why is that? Easy: remember that our condition was that collisions were elastic. After each collision, energy is conserved. Initial energy is,
\(E_{initial} = \frac{1}{2}M V_0^2\)
After \(j\)th collision, the total energy of two balls is,
\(E_{j} = \frac{1}{2}m(u^{(j)})^2 + \frac{1}{2}M(v^{(j)})^2\)
Equate the initial and final energies,
\(E_{initial} = E_{j} \)
\(\frac{1}{2} M V_0^2 = \frac{1}{2} m (u^{(j)})^2 + \frac{1}{2} M (v^{(j)})^2\)
aaaaand, simplify the equation a little bit,
\(V_0^2 = \alpha (u^{(j)})^2 + (v^{(j)})^2\)
This is an equation for an ellipse! To see its structure better, let me write \(x = \sqrt{\alpha}u^{(j)}\), \(y =v^{(j)}\) and \(V_0 = R\) for radius.
\(R^2 = x^2 + y^2\)
Which is equation for a circle. By counting the clanks, we start from the top, merge to right, then reflect the point on the right with respect to \(y\) axis and so on. At each two clanks (one collision and one reflection) the velocity of the big ball \(M\) decreases by \(2\alpha/(1+\alpha)\), until the velocity of \(M\) is close to \(-V_0\) and the small ball cannot catch it. So, if we let the \(\alpha<<1\), the whole process is nothing else than integrating the area under the ellipse. For a radius of \(R\), area of a circle is \(\pi R^2\). If the axes of an ellipse are \(a\) and \(b\), the area is \(\pi a b\), and if we elongate one of the axis by \(1/\alpha\), one of the axes become \(\sqrt{1/\alpha}V_0\) and other axis is just \(V_0\). Then the total area is proportional to \(\pi V_0 \sqrt{1/\alpha} V_0\propto V_0^2 \pi \sqrt{1/10^{-N}} \propto \pi \sqrt{10^{N}}\). There you go! (I will not say the archaic word Q.E.D.).
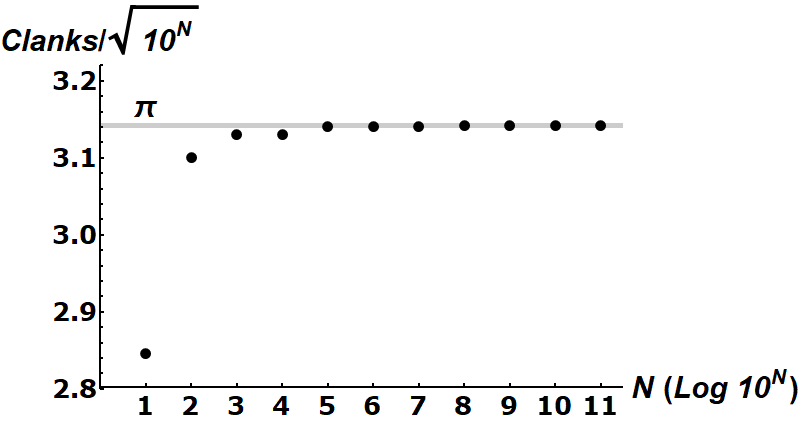
Here I plotted the exponent \(N\) vs. clank number/\(\sqrt{10^N}\). It converges to \(\pi\) pretty quickly.
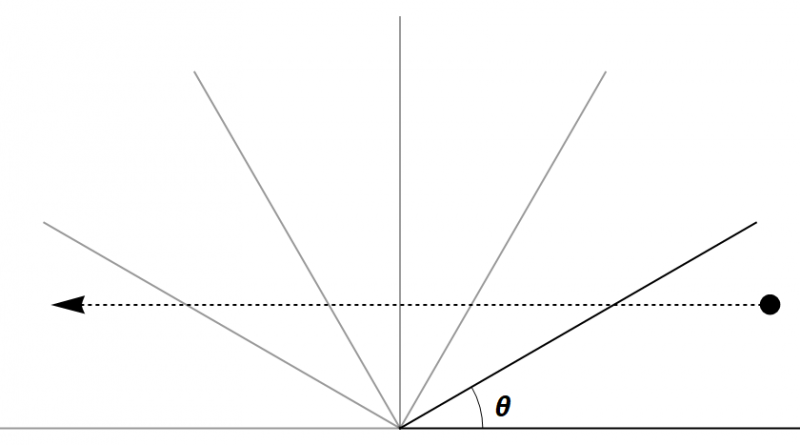
This problem is so beautiful, such that it is related to one other problem. This new problem is subject of the paper, G. Galperin, 2001, Regular and Chaotic Dynamics, V. 8, №4, (2003). Imagine you divide the upper-half plane by an angle \(\theta\), that is you made a wedge.
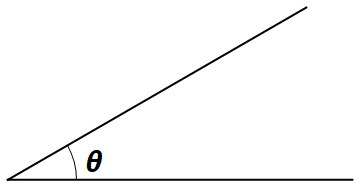
Then, you send a ball moving with initial velocity \(V_0\) towards this wedge.
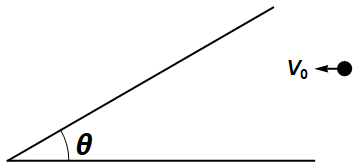
As the ball bounces back and forth of the walls of the wedge, how many times does the ball bounce?
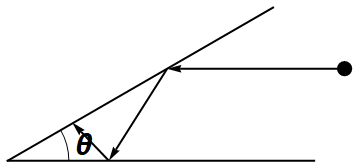
How is this problem related to the previous problem? Well, we were counting the clanks until the \(v^j\) is higher than \(u^j\), weren’t we? Many of those countings are actually redundant. We can only look for after how many clanks does the \(v^j\) is higher than \(u^j\) in one quarter, then multiply that by 4.
If we imagine our new ball, which goes into a wedge, as the point in \(u,\sqrt{\alpha}v\) space, we are looking for when this new ball passes π/4. If the masses were the same, this velocity space would be a circle:
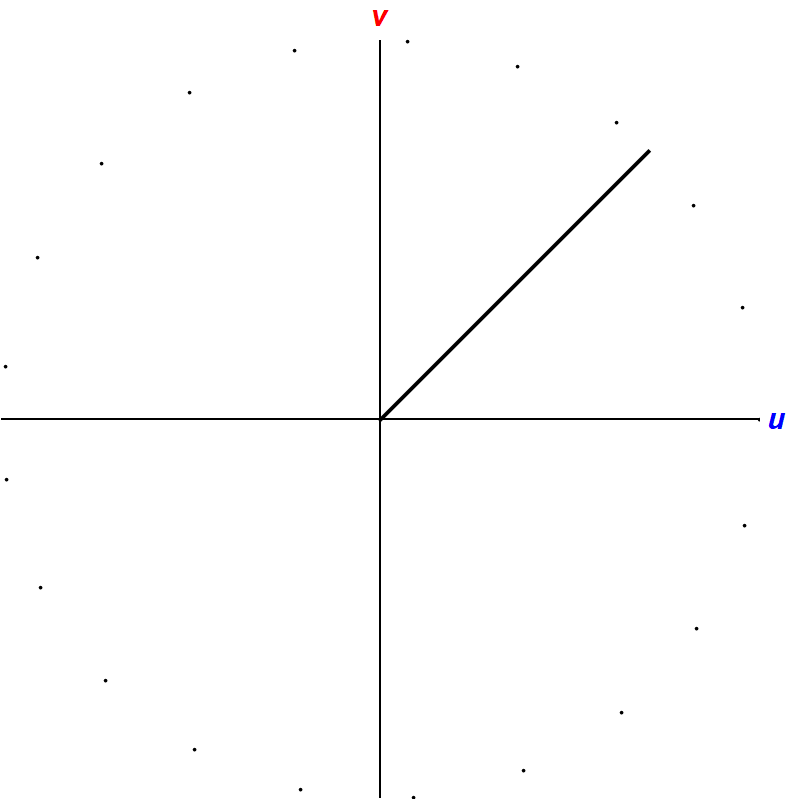
In elongated \(u,v\) space, of which is an ellipse, this \(\pi/4\) angle looks like a wedge of which the angle is \(\arctan \theta = \sqrt{m/M} = \alpha\).
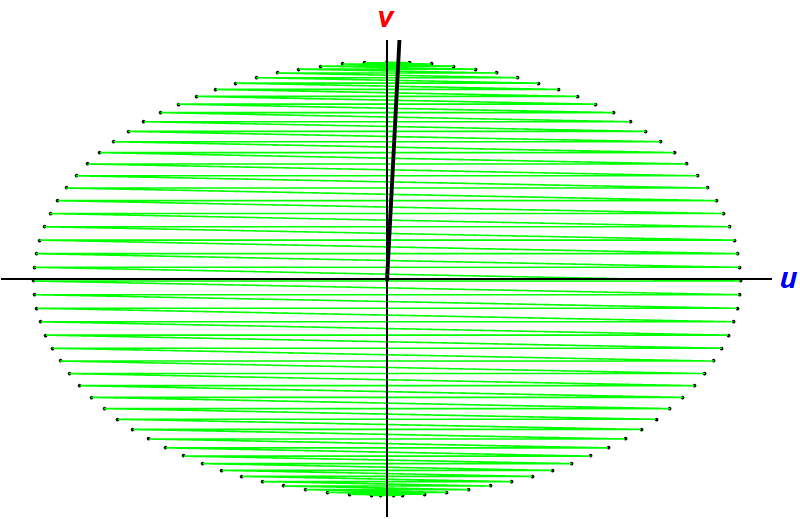
Now the question is: How many times does the ball bounce back and forth inside this narrow wedge? It might look like a hard problem, but we can simplify. Remember that our collision is elastic. So, the magnitude of the velocity of the ball does not change. It is always \(V_0\). If this ball reflects back and forth inside the wedge, only the direction of the velocity changes. Then, I can simplify this problem with the following:
How many times does a ball with horizontal velocity \(V_0\) cross wedges with angles \(\theta\), filling the upper-half plane?
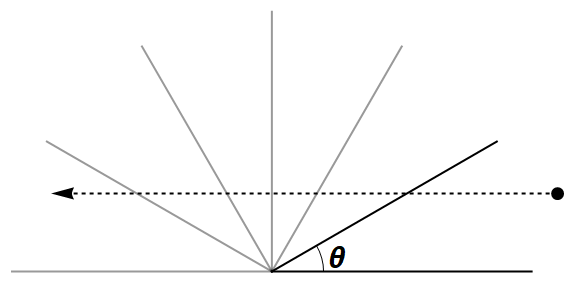
Well the answer is, \(\pi\sqrt{M/m}\) times!

Author, graphics: Doga M. Kurkcuoglu (Bilgecan Dede)
Doga Kurkcuoglu
Yazar: Doga Kurkcuoglu (tümünü gör)
- Bouncing Cubes and π (3Blue1Brown) - 14 January 2019
- Follow up to Fourier Series - 23 December 2018
- Purrier Series (Meow) and Making Images Speak - 11 December 2018



teşekkürler
Awesome…better than the original paper….and it’s also there in a YouTube channel
You are doing incredible work.. Saw your video with Smartereveryday. That was awesome too..
I loved your solution!
But it is not yet clear to me why the system will reach a “terminal state”. Although my intuition of physicist tells me that everything is perfectly fine, my mathematical side still needs clear proof of why the system cannot evolve indefinitely.
Hello,
I’m a student at the high school and I would like to say that, you do an very inspiring work ,to the extent that I’m doing my “year work” on the colliding blocs.
Can I ask you if you can show me how you solve the momentum conservation equation and the energy conservation equation to find:
v ′ = ((2m) / (M + m)) u + ((M − m) / (M + m)) v
u ′ = ((m − M) / (m + M)) u + ((2M) / (M + m)) v
Despite a lot of try, I havent been able to solve this equations with the right answer.
I’m looking foward for your response.
Sincerely a big fan of your work.
Dude thank you! This is extremely helpful!
Artykuł warty spędzonego czasu.
Film również obejrzałem, równie dobry.
Polecam
Beautiful mathematics and of course physics 😉
I to jest powód dla którego należy się uczyć matematyki.