Follow up to Fourier Series
I would like to first thank Destin Sandlin and then everyone for their support and interest. Here in this article I will try to answer couple of questions I have received with the video. Then, I guess I will not write about Fourier series for a while, since I have written about it a lot and I hate to repeat myself 🙂 I apologize that this article is going to be a little technical for a popular science blog.
Q1: Would it be possible to Fourier transform a polygon, i.e. square, pentagon etc?
Thank you Daniel Shiffman. Yes, since a regular polygon can be thought of a periodic curve, it can be expanded into Fourier series. Here I show how it can be expanded:
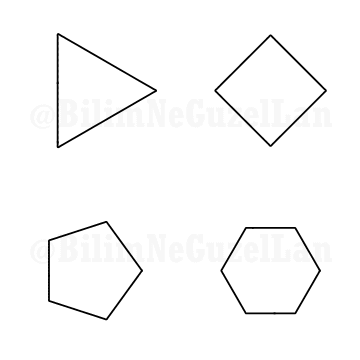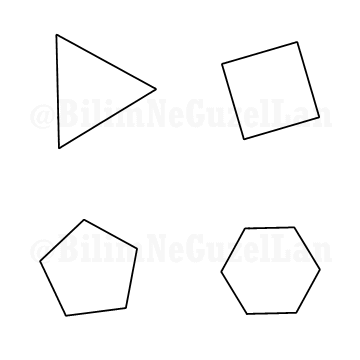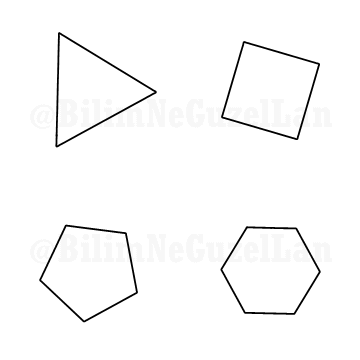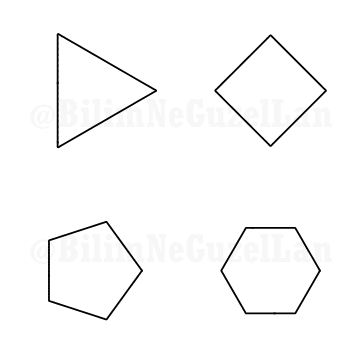
Assume \(f(x)\) represents the regular n-polygon.
Our goal is to expand this function \(f(x)\) into Fourier series:
\(\displaystyle{ f(x) =\frac{1}{2} a_0 + \sum \limits_{n} \left(a_n \cos(n x) + b_n \sin(n x)\right)}\)
But instead, let me write this Fourier series in other form, since carrying out the calculations will be easier:
\(\displaystyle{f(x) =\sum \limits_{m = -\infty}^{\infty} c_m e^{i m x}}\),
since \(e^x = \cos x + i \sin x\), where \(i = \sqrt{-1}\), imaginary number. OK, the punchline of Fourier analysis is to find the \(c_m\) coefficients.
\(\displaystyle{c_m = \frac{1}{2 \pi} \int \limits_{0}^{2\pi}f(x) e^{-i m x} dx}\)
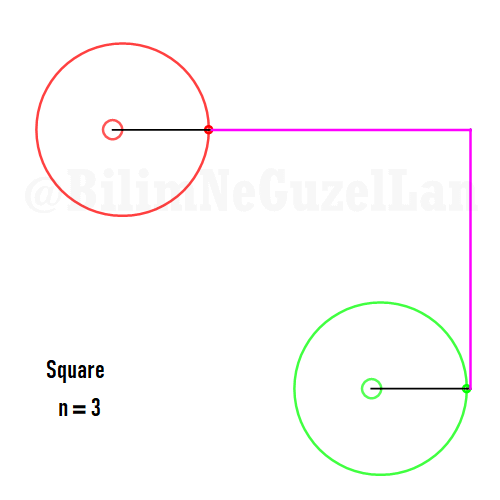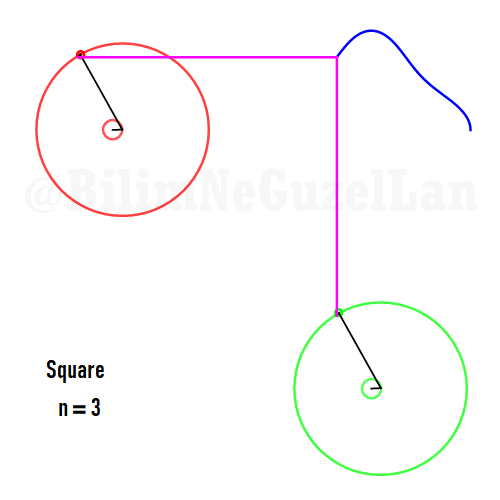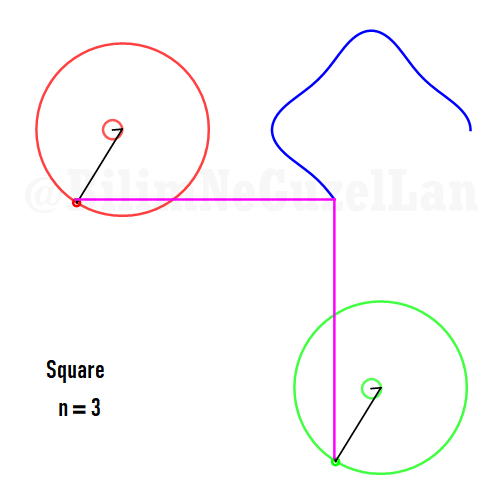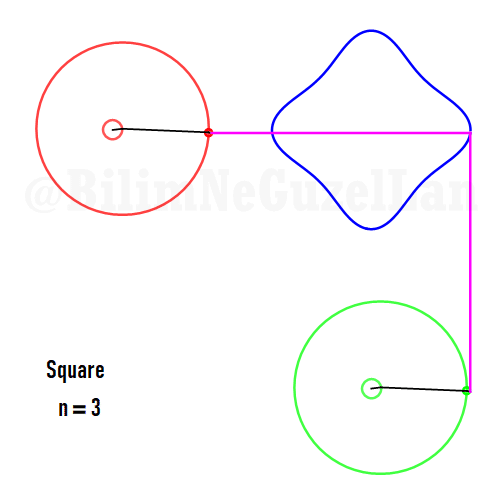
First thing I can do is to separate the polygon into n segments:
\(\displaystyle{c_m = \frac{1}{2 \pi} \sum \limits_{j = 0}^n \int \limits_{x_j}^{x_{j+1}}f(x) e^{-i m x} dx}\),
such that each integration is simply over a line. I can use integration by parts, and massage the terms a little bit:
\(\displaystyle{ \int \limits_{x_j}^{x_{j+1}}f(x) e^{-i m x} dx = \left.\left[f(x)\frac{e^{-im x}}{-i m}\right]\right|_{x_{j}}^{x_{j+1}} – \int \limits_{x_j}^{x_{j+1}}s_j \frac{e^{-im x}}{-i m}dx}\).
Where \(s_j \) is the slope of \(f(x)\) at the \(j\)th segment, \(s_j = df/dt\), which is a constant! As I take the summation over all segments of the polygon, the first term vanishes, since our starting point is that \(f(x)\) is periodic! We are left with the second term. But it is trivial to solve:
\(\displaystyle{c_m = \frac{1}{2 \pi} \sum \limits_{j = 0}^n \int \limits_{x_j}^{x_{j+1}}s_j\frac{e^{-im x}}{i m} dx} = -\frac{1}{2\pi m^2} \sum \limits_{j = 0}^n \sigma_j e^{-i m x_j} \),
where \(\sigma_j = s_j – s_{j-1}\). But, since again it is periodic, \(s_0 = s_n\). From this, we can find the \(n\)th slope by,
\(s_{j-1} = \frac{1}{2\pi}\sum \limits_{j = 0}^{n-1}x_j \sigma_j\).
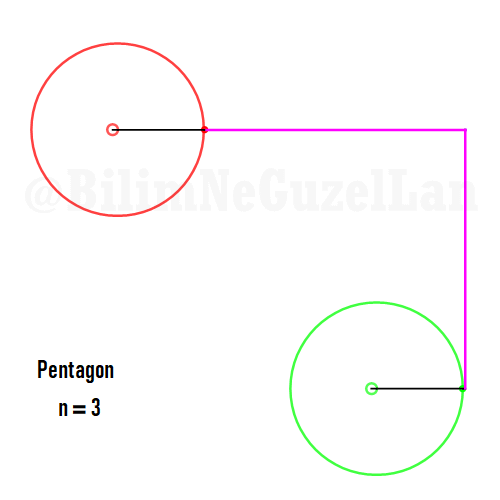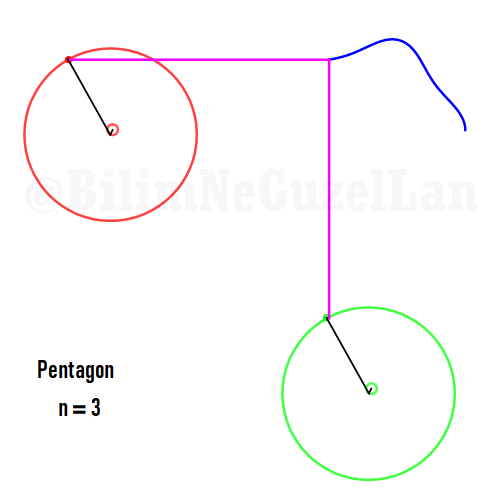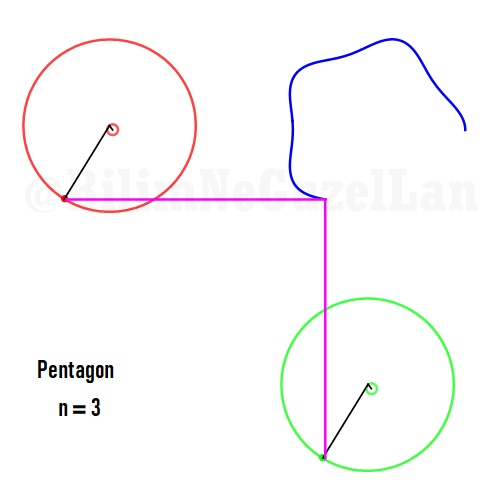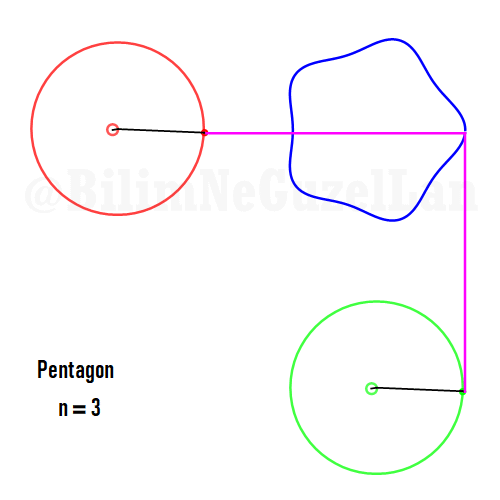
Now I will add animations of some of the polygons according to the rules I have described above. The real part will be the \(x\), and imaginary part will be the \(y\) component. Since I want to center the polygon, I have set \(j = 0\) term to be zero. Because of this, I can change the summation slightly:
\(\displaystyle{f(x) =\sum \limits_{l = 1 mod 2n} \frac{e^{i (2 + n l) x}}{(2+ nl)^2}}\)
Here are some of the polygons in Fourier series:
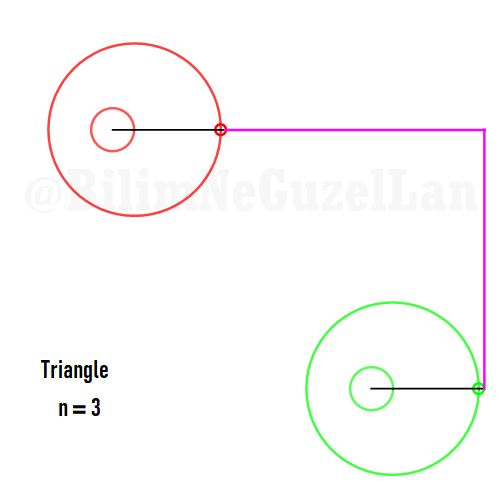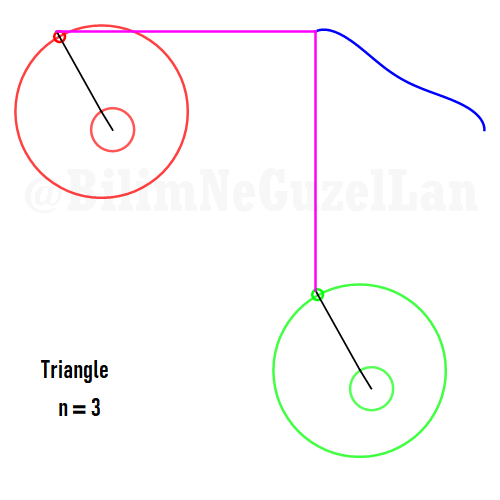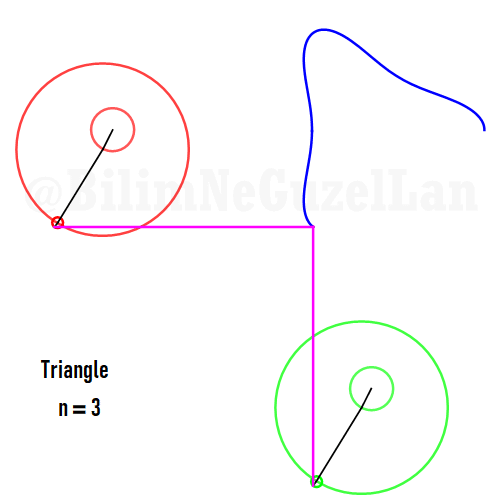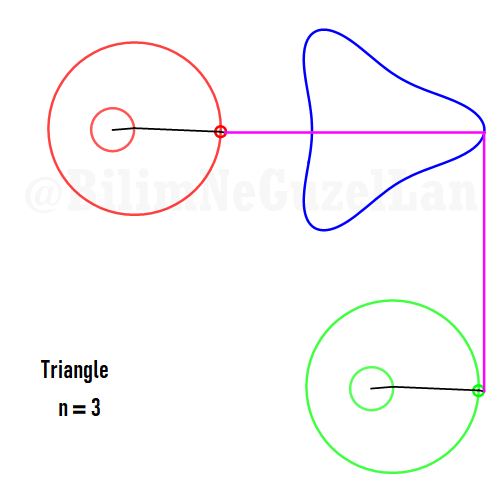
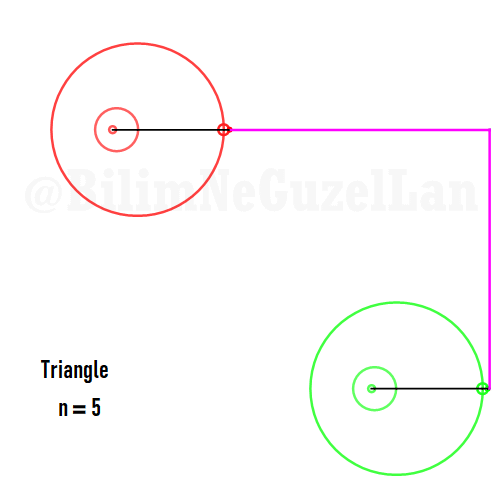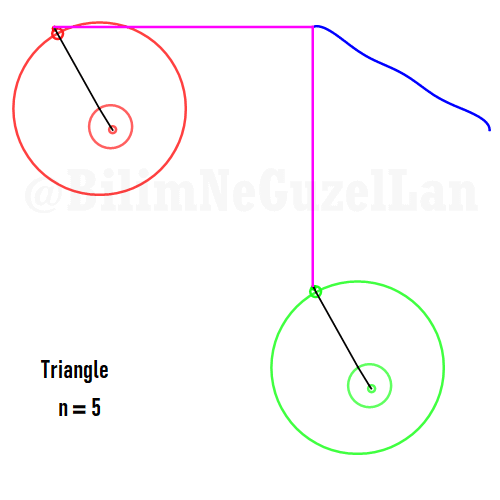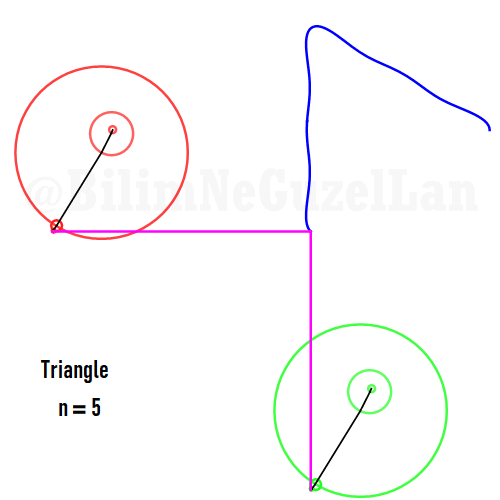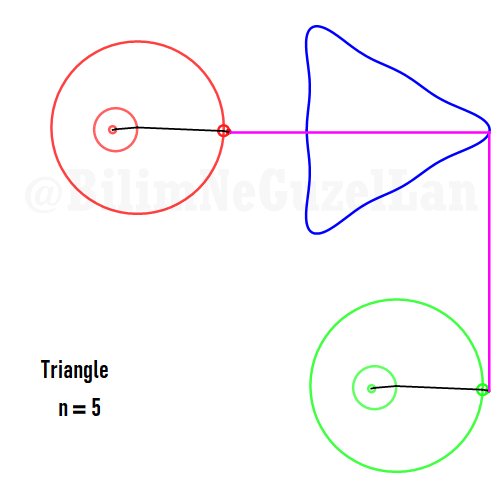
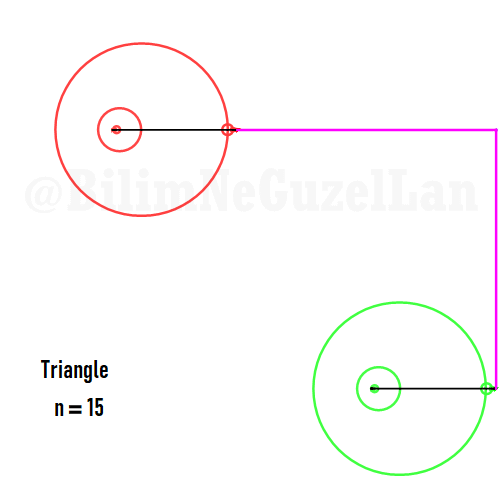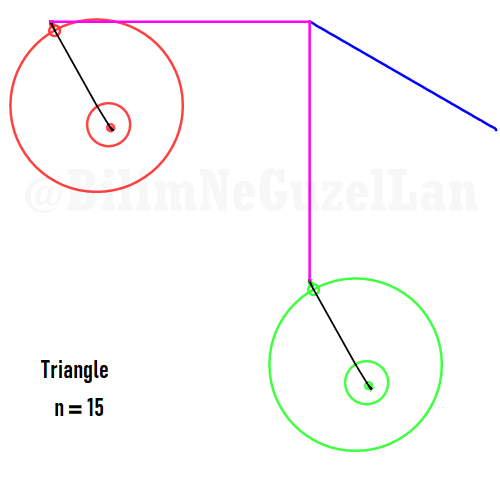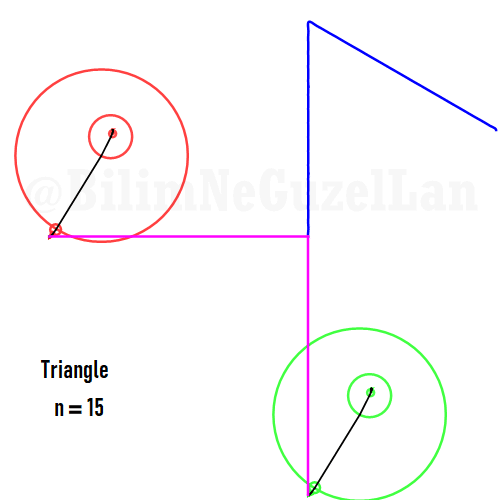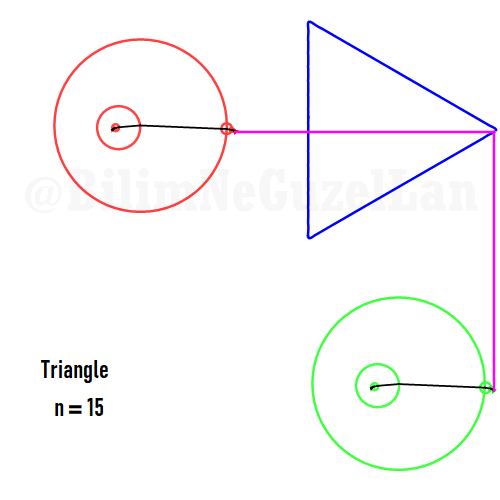
Square:
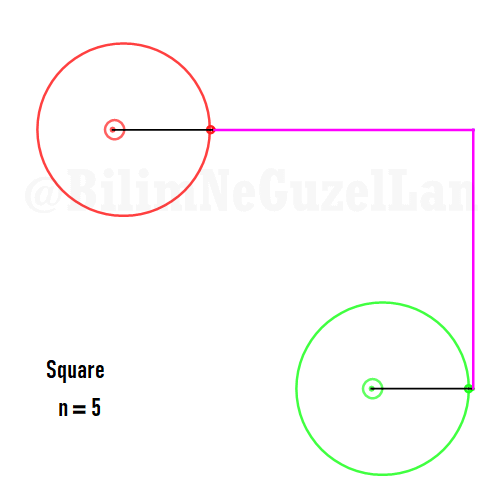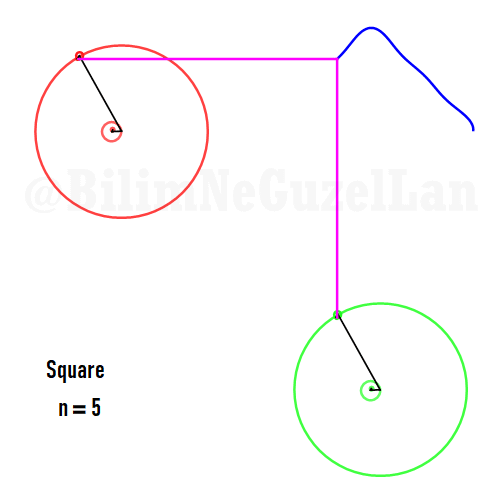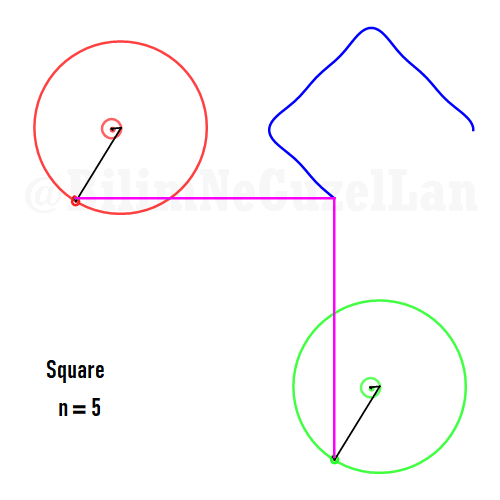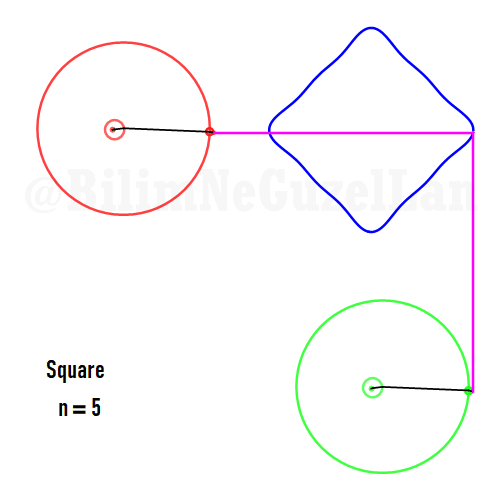
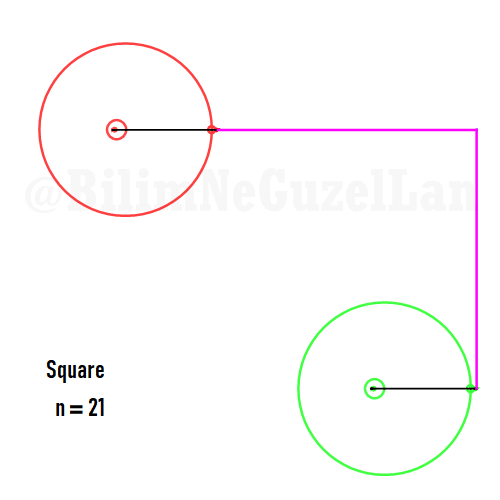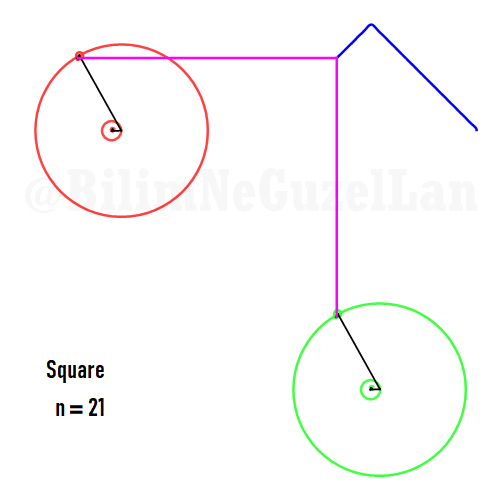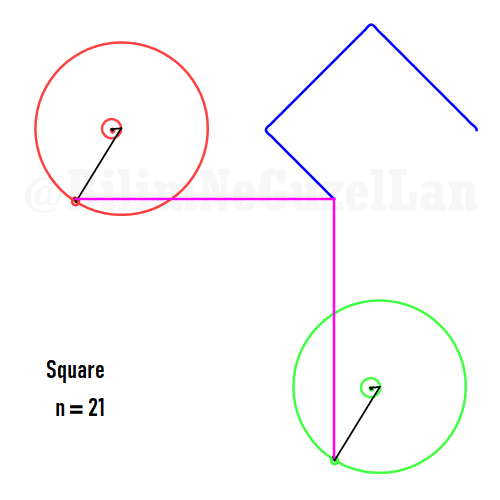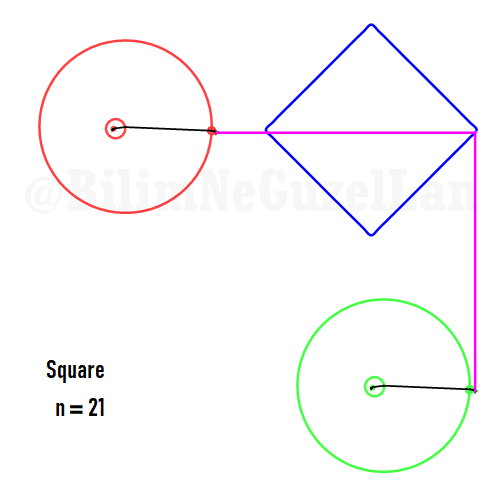
Pentagon:
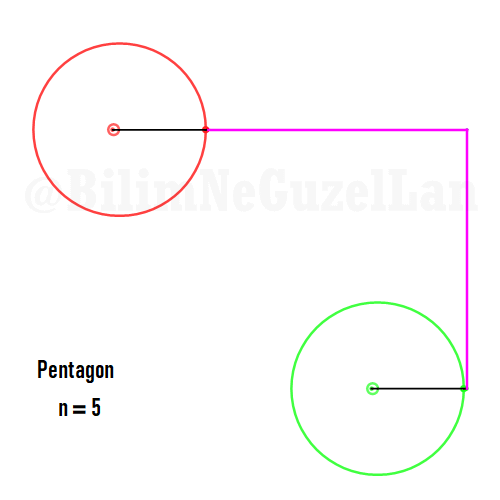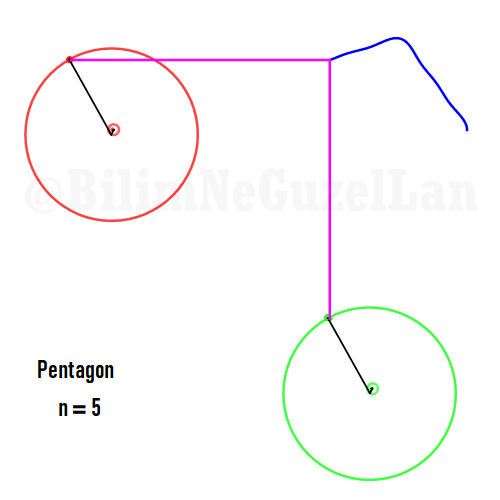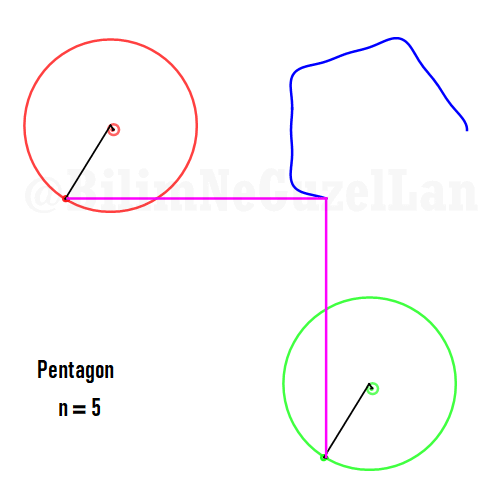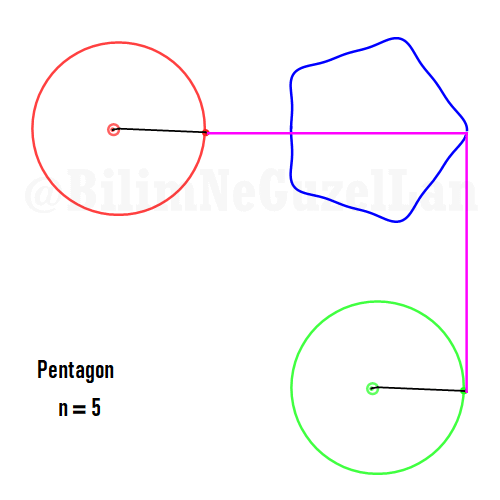
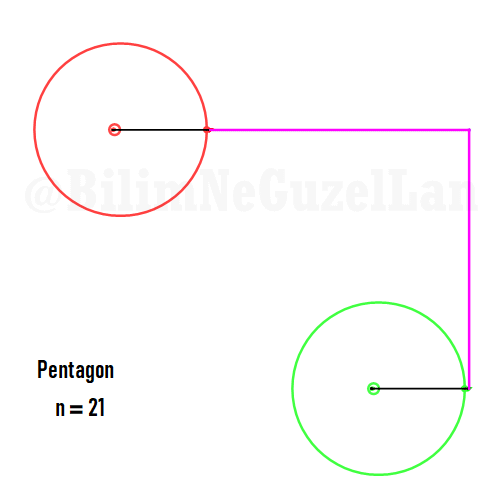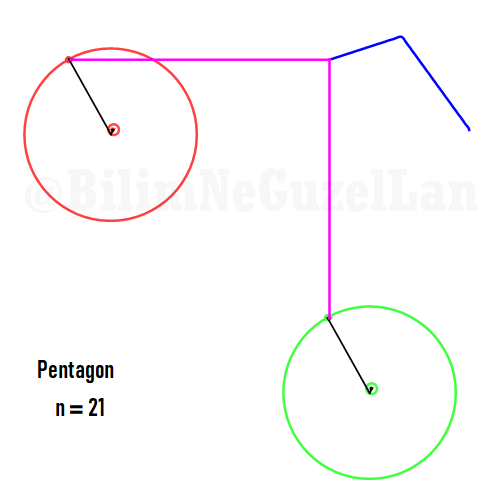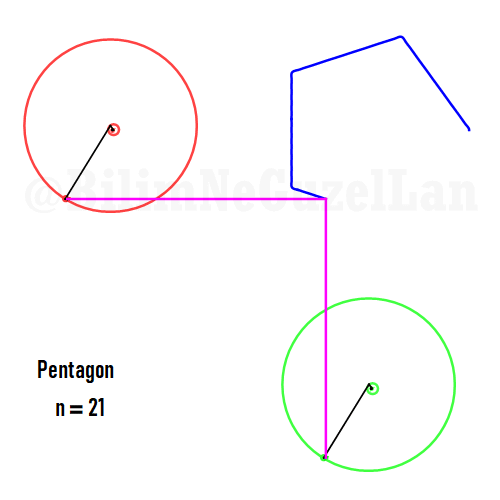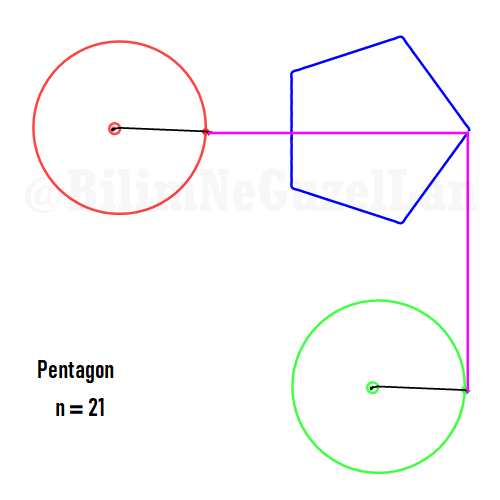
It is also possible to generate some cooler shapes, such as stars etc. One only needs to take the superposition of two polygons with asymmetric harmonics, that is no common divisor between \(n_1\) and \(n_2\):
\(\displaystyle{f(x) =\sum \limits_{l = 1 mod 2n} \frac{e^{i (n_1 + n_2 l) x}}{(n_1+ n_2 l)^2}}\)
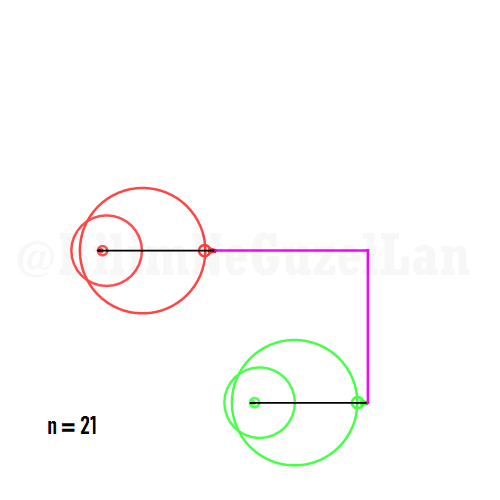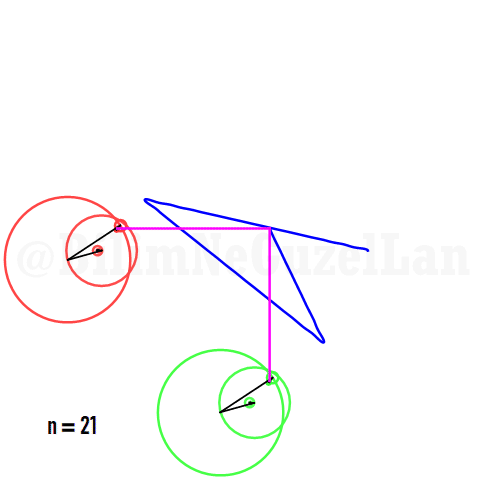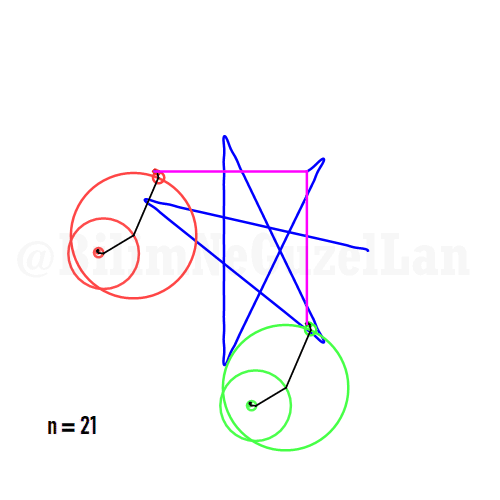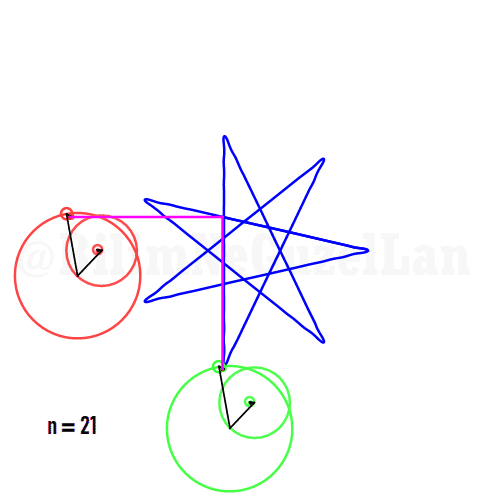
Here I generate one such shape, a star:
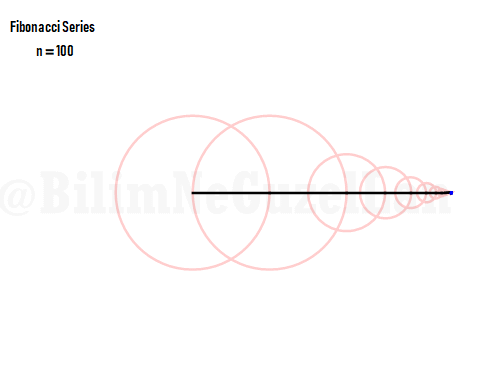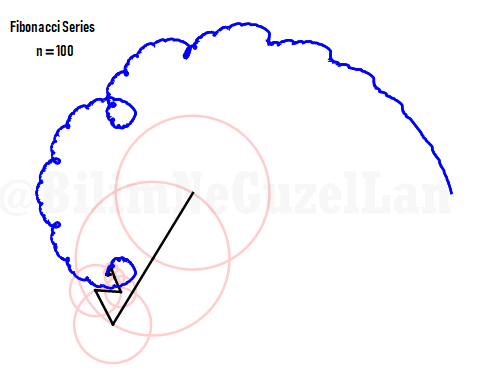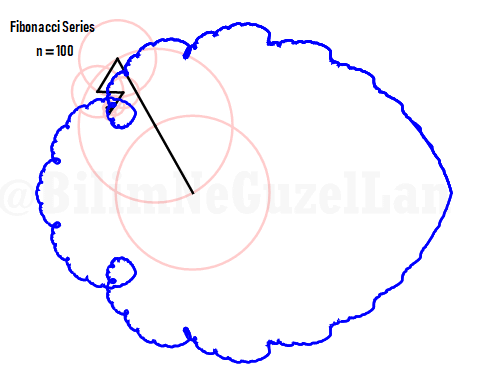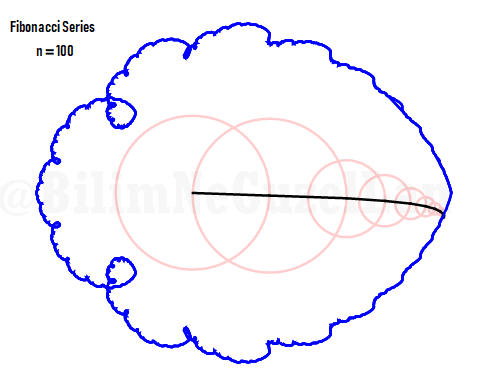
Q2: How would the function look like if harmonics follow Fibonacci series, i.e. 1, 1, 2, 3, 5, 8, 13, 21, etc.?
Thank you Laura Kinnischtzke for the suggestion. Here how it looks like in polar form,
\(\displaystyle{ f(\theta) = \sum \limits_{n \in F_n} \left(\frac{c}{n} \cos(n \theta) + \frac{c}{n} \sin(n \theta) \right)}\)
where \(F_n = F_{n-1} + F_{n-2}\), which is Fibonacci set.
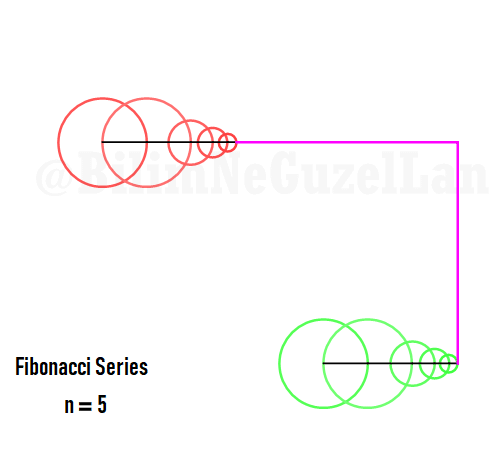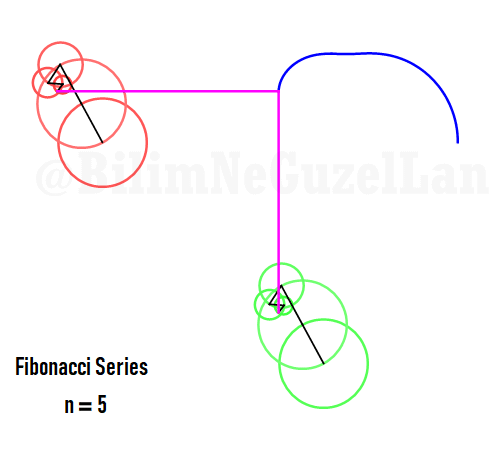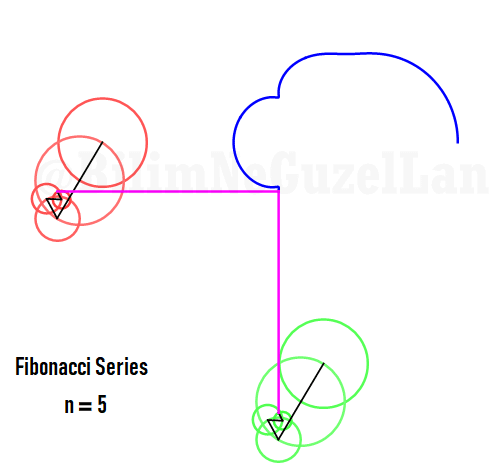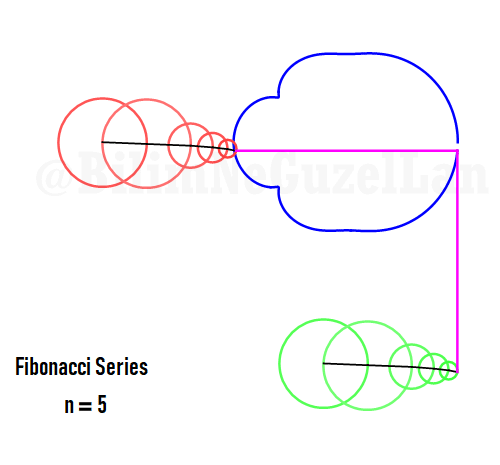
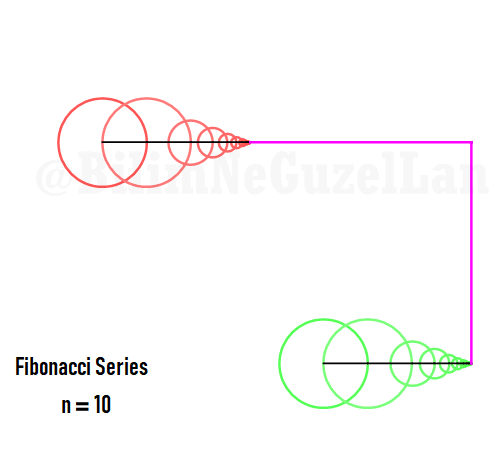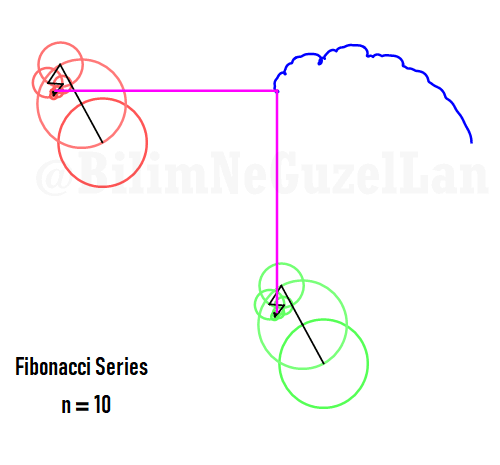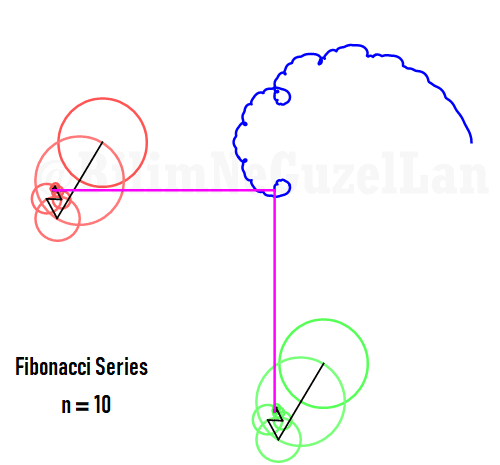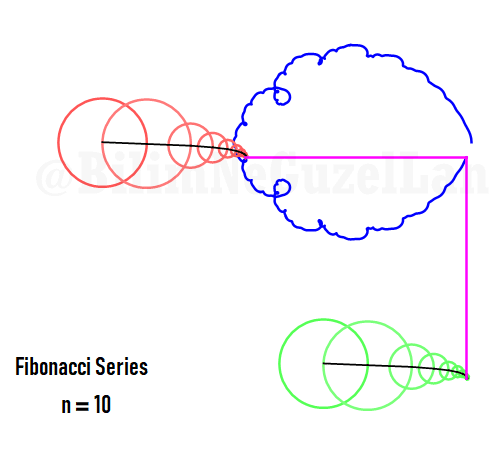
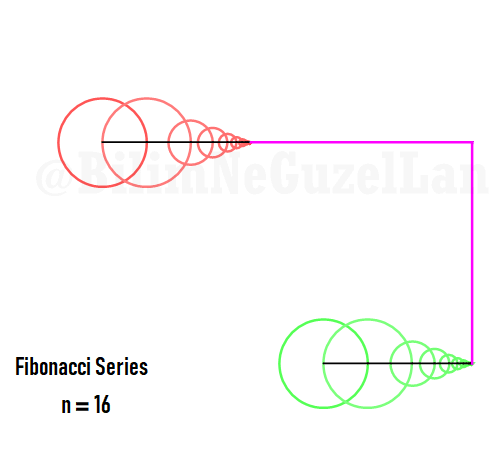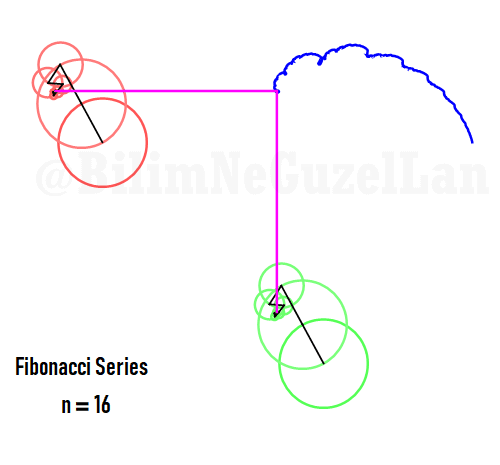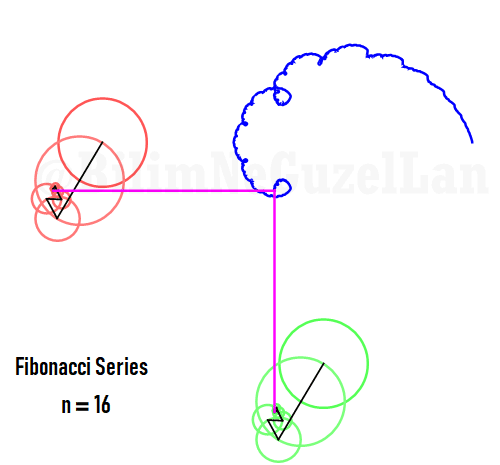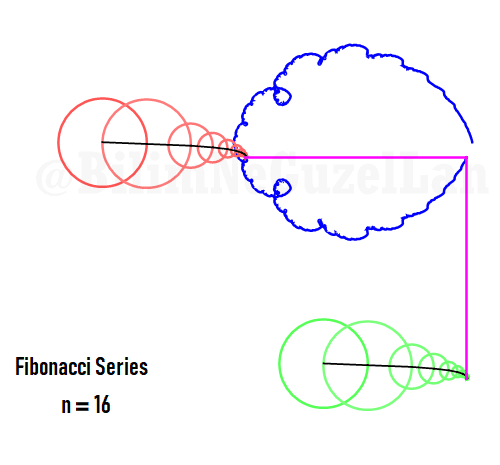
The function in one period is a fractal, and looks like a Weierstrass function:
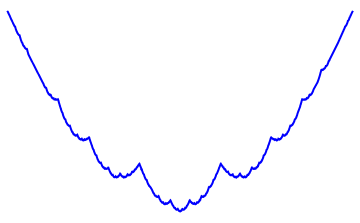
…and here is the 100 harmonics added, just because I can (it looks cool).
Animations: Doga Kurkcuoglu (Bilgecan Dede)
Doga Kurkcuoglu
Yazar: Doga Kurkcuoglu (tümünü gör)
- Bouncing Cubes and π (3Blue1Brown) - 14 January 2019
- Follow up to Fourier Series - 23 December 2018
- Purrier Series (Meow) and Making Images Speak - 11 December 2018



The Fibonacci series function looks like a brain seen from above! (Have you ever heard about human connectome project? http://www.humanconnectomeproject.org/ – I think it could be really interesting if you “read” the numeric function of the brain pathways )
Really great follow-up to your previous work…Inspiring!! Thank you!
-Carl Schell – Michigan, USA
Poga – Can you model the “Golden Ratio” and “Fibonacci Numbers” to see if you can get square waves to form?
– What is a Fourier Series? (Explained by drawing circles) – Smarter Every Day 205 –
A great Youtube video above ^
Hi,
Thank you for this awesome tutorial, can you please give more details about the part (We are left with the second term. But it is trivial to solve).
Hi,
Thanks for your great post. I am trying to fit a curve to the profile of a gear-shaped geometry using the FFT analysis. Can you give me some guidance on how to select my base equation?
I can provide more information on the shape I’m trying to fit a curve to.
what about 1000 harmonics then?
ooooh man.. you made me love math again.. I started hating it when I was not able to understand !!! I should put some interest in maths again..
Would you please suggest me.. where should I begin learning again.. I’m a software engineer btw, and understand enough basic visual “methematics”.. but you ‘ve killllled me.
Mükemmel bir çalışma olmuş, elinize sağlık. Odtü ee de okuyorum ancak sizin anlattığınız kadar net okulda anlayamamıştım sağolun.
Amazing work.
About Fibonacci did you know this property of the golden rectangle built using fibonacci numbers 1 1 2 3 5 8 … ?
http://lambdaway.fr/workshop/?view=fibonacci
Your opinion is welcome.
Regards
Alain Marty
hi every body.H(ve liked your works about Fourier’s Series and I Hope send me the source file of all your work’s.thenk you from Algeria.
Hi,
Can you use these methods to find a solution to the Bessler Wheel?
http://Www.besslerwheel.com
Thanks
Damian
Hi,
Can you use these methods to find a solution to the Bessler Wheel?
http://Www.besslerwheel.com
Thanks
Damian
I cannot understand what the two circles mean and how they are related to the Fourier series.
Is there a software that will allow me to input the number of vectors and their amplitude as well as the spin direction and speed, and outputs the picture being created.
Thanks for your awesome blog. Pl. give us a series for a heart-shaped curve with the amplitude and frequency of each term.
This is my first visit. These days I am learning about Fourier series and while I as searching Youtube and found a post by ‘SmarterEveryday’ channel and that led me here. This is a fantastic blog. From now on I will study the contents of this blog. Animation is amazing. Concept is much more amazing. Thank you.
Visualization of Fourier sum is very Interesting. I became to know that you used Mathematica package to write the animation program. I also did some Fourier series stuff for various periodic curves using Mathematica. My usage is only up to Manipulate[ ] command. They are nowhere near our animation. For some curves I summed up to 100,000 terms. I Wish I have your animation program. I am still learning Mathematica and Fourier series. Your series is great. Thank you.
Hi , great work bro !
Love from Nepal
To świetny artykuł! Ciekawie pokazuje, jak Fourier może być zastosowany do analizy kształtów, co pozwala na wizualizację matematyki w zupełnie nowy sposób. 🌟 Rozkładanie wielokątów na szeregi Fouriera to doskonały przykład na to, że matematyka może być zarówno techniczna, jak i artystyczna. Animacje, które przedstawiasz, naprawdę ożywiają te koncepcje! A pomysł zastosowania szeregów Fibonacciego do generowania kształtów tylko dodaje smaku tej matematycznej mieszance! Czekam z niecierpliwością na więcej takich innowacji! 🔍💡