1/3 Nerede ya da Kaos’a Giriş
Kaos, matematiğin oldukça yeni kuramlarından biridir. Kaos, kargaşa anlamına gelen Yunanca kökenli bir sözcüktür.
Kaos kuramını biraz açıklamaya çalışayım.
Şöyle kuvvetlice öksürün. Atmosferde küçücük bir değişiklik yaptınız, hafif bir dalgalanma oldu: Hava alıp verdiniz. Bu küçük atmosfer değişikliğinin bugün ya da yarın sonuçlarını göremeyebilirsiniz. Ama bir yıl sonra, o kuvvetli öksürüğünüz Bengladeş’te evleri yerle bir eden bir tayfuna neden olabilir. Belki… Bilinmez… Ya da bir kelebeğin şöyle bir kanat çırpmasının on yıl sonra doğuracağı sonuçları bilemeyiz.
Bu yüzden meteoroloji yalnızca bir haftalık tahmin yapabilir, bir yıl sonrasını tahmin edemez.
Birbirine çok yakın koşullar, çok uzun bir süre sonra birbirine hiç benzemeyen durumlar yaratabilir.
İşte kaos kuramı bu sorunla ilgilenir.
Matematikte kaos/kargaşa var mıdır? Evet vardır. Var ki kuramı bulunmuş.
Matematikten bir kaos örneği vereceğim bu yazımda.
1/3’ün tam nerede olduğunu hiç merak ettiniz mi? 1/3’ün nerede olduğunu bulmaya çalışacağız.
Şurası kesin ki, 1/3, sıfırla bir arası bir sayıdır , yani [0, 1] aralığındadır. 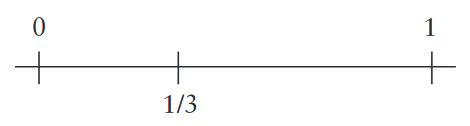
Ama bunu bilmek 1/3’ün tam nerede olduğunu bilmek değildir. 1/3’ün tam nerede olduğunu biraz daha iyi anlayalım.
[0, 1] aralığını ortadan ikiye bölersek, 1/3 hangi tarafa düşer? Sağa mı, sola mı? Yani 1/3, 1/2’den küçük müdür, büyük müdür? Elbet 1/3 < 1/2 eşitsizliği geçerlidir ve 1/3 soldaki aralığa düşer.
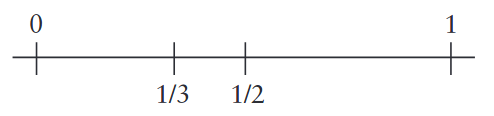
Yukarda, [0, 1] aralığını tam ortadan ikiye bölüp, [0, 1/2] ve [1/2, 1] aralıklarını elde ettik ve gördük ki 1/3 sayısı [0, 1/2] aralığındaymış, yani, 0 1/3 1/2 eşitsizlikleri geçerliymiş. Şimdi, 1/3’ün bulunduğu [0, 1/2] aralığını tam ortadan ikiye bölelim:
[0, 1/4] ve [1/4, 2/4]
aralıklarını elde ederiz. 1/3 sayısı bu aralıklardan hangisine düşer? Sola mı, sağa mı? 1/4 1/3 2/4 eşitsizlikleri geçerli olduğundan, 1/3 sayısı ikinci aralıktadır, yani [1/4, 2/4] aralığındadır, yani sağa düşer.
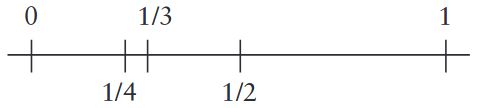
Şimdi [1/4, 2/4] aralığını ikiye bölelim.
[2/8, 3/8] ve [3/8, 4/8]
aralıklarını elde ederiz. 2/8 < 1/3 < 3/8 eşitsizlikleri geçerli olduğundan, 1/3 sayısı birinci aralığa, yani sola düşer.
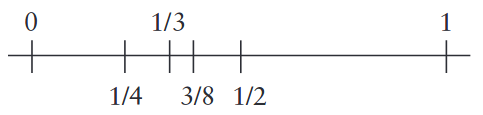
Ya [2/8, 3/8] aralığını ikiye bölecek olursak? Ve böyle devam edecek olursak?..
Genel olarak, [0, 1] aralığını 2n tane eşit uzunlukta aralığa bölecek olursak, 1/3 bu aralıklardan hangisine düşer?
Yanıtı vereyim. 1/3 sayısı, ortadan bölünen aralıkların bir soluna, bir sağına düşer. Yani, 1/2’nin soluna, 1/4’ün sağına, 3/8’in soluna, 6/16’nın sağına…
Kaos bunun neresinde?
1/3 = 0,333333… eşitliğini biliyoruz. 0,333333 sayısı 1/3’e çok yakın bir sayıdır ama 1/3 değildir. 0,333333 sayısı da başlangıçta 1/3 gibi bir sola, bir sağa düşer ama bir zaman sonra 1/3’ün davranışından tamamıyla uzaklaşır, sanki 1/3’le uzaktan yakından bir ilgisi yokmuş gibi davranır. İşte bu kaostur. Birbirine çok yakın iki sayı, bir süre benzer biçimde davranırlar ama bir süre sonra birinden alınan bilgi, öbürü hakkında bize hiçbir bilgi vermez.
1/3’ün nerde olduğuna geri dönelim. Aşağıdaki eşitliklerin bir kısmını bulduk, bulmadıklarımızın da doğru olduklarını kontrol etmek pek zor değildir:
n kaç olursa olsun, öyle bir an tamsayısı vardır ki,
an/2n ≤ 1/3 ≤ (an+1)/2n (1)
eşitsizlikleri geçerlidir. Yukardan da anlaşılacağı üzere,
a1= 0
a2= 1
a3= 2
a4= 5
a5= 10
a6= 21
a7= 42
eşitlikleri geçerlidir. Bundan sonraki sayıları bulmak da pek güç değil, dizi şöyledir: 0, 1, 2, 5, 10, 21, 42, 85, 170, 341, 682… Bu dizinin sonraki sayılarını okur kolaylıkla tahmin edebilir. Ama elbet, tahmin yalnızca bir tahmindir. Bu tahminin kanıtlanması gerekmektedir.
Şimdi,
n tekse, an çifttir
n tekse, an tektir.
önermesini kanıtlayacağız.
Her şeyden önce, (1) eşitsizliklerinde eşitliğin olamayacağını kanıtlamamız gerekiyor. Gerçekten de, bir a tamsayısı için, a/2n = 1/3 ise, 3a= 2n eşitliği de geçerlidir ve bundan da 3’ün 2n’yi böleceği çıkar ki, bu doğru değildir. Dolayısıyla (1) eşitsizliklerini daha keskin bir biçimde,
an/2n < 1/3 < (an+1)/2n
olarak yazabiliriz. Bu eşitsizliklerdeki sayıların paydalarını temizleyelim, yani sayıları 3 x 2n ile çarpalım:
3an < 2n < 3an+3
eşitsizliklerini elde ederiz. Dolayısıyla 2n sayısı 3an’den büyük, ama 3an+3’ten küçük bir sayıdır. 3an’den büyük ve 3an+3’ten küçük iki sayı vardır: 3an+1 ve 3an+2. Demek ki 2n sayısı bu iki sayıdan birine eşittir:
Ya 2n= 3an+1 ya da 2n= 3an+2. (2)
Bunlardan hangisi doğru? n’nin tekliğine ya da çiftliğine göre değişir yanıt. Eğer n çiftse 2n= 3an+1, tekse 2n= 3an+2 eşitliği geçerlidir. Neden? Nedenini birazdan söyleyeceğim. Önce biraz ön bilgiye gerek var.
Önce şu biline: 2n-2, 2n-1 ve 2n sayıları üç ardışık sayıdır. Dolayısıyla içlerinde biri, ve yalnızca biri üçe bölünür. 2n sayısı üçe bölünmediğinden, 2n-2 ve 2n-1 sayılarından birinin, ve yalnızca birinin üçe bölündüğü anlaşılır.
Sav. Eğer n çiftse, 2n-1 üçe bölünür. Eğer n tekse, 2n-2 üçe bölünür.
Savın Kanıtı: Önce n’nin çift olduğunu varsayalım ve n’yi 2m biçiminde yazalım:
n= 2m.
2m-1, 2m ve 2m+1 sayıları üç ardışık sayı olduğundan, biri üçe bölünür. Ama 2m üçe bölünmez elbet. Demek ki 2m-1 ve 2m+1 sayılarından biri üçe bölünür. Bunu aklımızda tutalım, bir sonraki paragrafta gerekecek.
Sonra şu basit hesabı yapalım:
2n-1 = 22m-1 = (2m)2-1 = (2m-1)(2m+1).
Bu eşitliğin sağ tarafındaki 2m-1 ve 2m+1 sayılarından birinin üçe bölündüğünü biraz önce görmüştük. Demek ki çarpımları da, yani 2n-1 de üçe bölünür. Savımızın birinci bölümünü kanıtladık.
Şimdi n’nin bir tek sayı olduğunu varsayalım ve n= 2m+1 yazalım. Gene hesaplayalım:
2n-2 = 22m+1-2 = 2(22m-1).
Biraz önce 22m-1’in üçe bölündüğünü görmemiş miydik? Demek ki yukarıdaki eşitliğin sayıları da üçe bölünürler, yani 2n-2 de üçe bölünür.
Savımız kanıtlandı.
Şimdi (2)’ye geri dönelim.
Eğer 2n= 3an+1 eşitliği geçerliyse, 3an= 2n-1 eşitliği de geçerlidir, yani 2n-1 üçe bölünür (dolayısıyla 2n-2 üçe bölünmez.) Yukarıdaki savdan da n’nin çift olduğu anlaşılır.
Eğer 2n= 3an+2 eşitliği geçerliyse, 3an= 2n-2 eşitliği de geçerlidir, yani 2n-2 üçe bölünür (dolayısıyla 2n-1 üçe bölünmez.) Yukarıdaki savdan da n’nin tek olduğu çıkar.
Demek ki,
n çiftse, 2n= 3an+1
n tekse, 2n= 3an+2
önermesini kanıtladık, yani,
n çiftse, an= (2n-1)/3
n tekse, an= (2n-2)/3
önermesini kanıtladık. Ne güzel!
Şimdi an’nin tekliği-çiftliği konusuna dönelim.
Eğer n çiftse, yani an= (2n-1)/3 ise, an ikiye bölünemez çünkü 2n-1 ikiye bölünemez. Dolayısıyla bu şıkta an tektir.
Eğer n tekse, yani an= (2n-2)/3 = 2(2n-1-1)/2 ise, elbette an ikiye bölünür.
Bu da 1/3 sayısının aralıkların bir soluna bir sağına düştüğünü gösterir.
Son olarak aşağıdaki güzel eşitliği kanıtlayayım:
1/3 = 1/2-1/4+1/8-1/16+1/32-1/64+… (3)
Bu eşitliğin sağındaki toplam sonsuz bir toplamdır.
Sağdaki sonsuz toplama x diyelim:
x= 1/2-1/4+1/8-1/16+1/32-1/64+…
Şimdi x’i ikiyle çarpalım:
2x = 2(1/2-1/4+1/8-1/16+1/32-1/64+1/128-1/256+…)
= 1-1/2+1/4 –1/8+1/16-1/32+1/64 –1/128+…
= 1-(1/2 –1/4+1/8-1/16+1/32-1/64+1/128-…)
= 1-x.
Yani 2x = 1-x. Bundan da kolaylıkla x= 1/3 çıkar!
(3) eşitliği kanıtlanmıştır.1
Bu kanıt sizi (3) eşitliğine inandıramadıysa hesaplayın:
1/2 = 0,5
1/2–1/4 = 0,25
1/2–1/4+1/8 = 0,375
1/2–1/4+1/8–1/16 = 0,3125
1/2–1/4+1/8–1/16+1/32 = 0,3475
1/2–1/4+1/8–1/16+1/32–1/64 = 0,328125
1/2–1/4+1/8–1/16+1/32–1/64+1/128 = 0,3359375
1/2–1/4+1/8–1/16+1/32–1/64+1/128–1/256 = 0,33203125
1/2–1/4+1/8–1/16+1/32–1/64+1/128–1/256+1/512 = 0,333984375
1/2–1/4+1/8–1/16+1/32–1/64+1/128–1/256+1/512–1/1024 = 0,3330078125
1/2–1/4+1/8–1/16+1/32–1/64+1/128–1/256+1/512–1/1024+1/2048 = 0,33349609375
1/2–1/4+1/8–1/16+1/32–1/64+1/128–1/256+1/512–1/1024+1/2048–1/4096= 0,333251953125
1/2–1/4+1/8–1/16+1/32–1/64+1/128–1/256+1/512–1/1024+1/2048–1/4096+1/8192= 0,3333740234375.
Görüldüğü gibi, işlemleri yaptıkça 0,3333… sayısına, yani 1/3’e yaklaşıyoruz. işlemleri sonsuza dek yapmaya zamanımız olsaydı, tam 1/3 bulurduk. işlemleri sonsuza dek yapamasak bile, yukarda yaptığımız gibi, sonsuz işlemin sonucunun 1/3 olduğunu matematikle buluruz.
Yazının birinci bölümündeki sorunun yanıtı, (3) eşitliğinden de bulunabilir.
Dileyen okur “1/5 nerde?” sorusunu yanıtlayabilir.2

1 : Burada biraz yalan söylüyorum. Eğer sonsuz toplamın sonucu sonlu bir sayıysa kanıt geçerlidir.
2 : Bu yazının kaosla ilgili olduğunu bana öğreten Tayfun Akgül’e teşekkürler.
Kaynak : Matematik ve Sonsuz
Yazar: Ali Nesin (tümünü gör)
- Matematik ve Doğa - 18 Aralık 2019
- Loto! - 25 Eylül 2019
- Cemal Amca’nın Zarları - 29 Ağustos 2019
- Şapka Problemi - 15 Ağustos 2019
- Çok Basit Aritmetiğe Çok Basit Bir Çözüm - 1 Ağustos 2019