Şapka Problemi
Bu ayın konusu olan problem Amerika’da bayağı heyecan yaratmış. Hatta Amerika’nın en saygıdeğer gazetelerinden biri olarak kabul edilen The New York Times’da uzun bir yazıya konu olmuş. Bu yazının ilk kısmı da The New York Times’da yayımlanan o yazıdan kaynaklanmıştır.
Şapka Problemi adıyla bilinen bu problem şöyle.
Bir odaya n kişi girecek. Odada bu kişilerin başlarına yazı tura atarak beyaz ya da siyah şapka konacak. Yani herkesin başında yüzde elli beyaz şapka olacak, yüzde elli siyah şapka. Herkes başkasının başındaki şapkanın rengini görecek ama kimse kendi başındaki şapkanın rengini göremeyecek… Oyuncular aynı anda ya kafalarındaki şapkanın rengi konusunda bir tahminde bulunacaklar ya da pas geçecekler. Eğer hiçbiri yanılmazsa (pas geçen hiç yanılmaz!) ve aralarından en az biri doğru yanıt verirse her oyuncu 1 milyon dolar alacak. Yoksa herbiri hava alacak.
Örneğin biri dışında hepsi pas geçerse ve o pas geçmeyen (camgöbeği ya da fıstıki gibi herhangi bir tahminde değil!) siyah ya da beyaz tahmininde bulunursa, yüzde 50 olasılıkla her oyuncu 1 milyon dolar alacak, yüzde elli olasılıkla kimse para kazanamayacak.
Eğer iki kişi pas geçmeyip tahminde bulunursa, o zaman yüzde 25 olasılıkla oyuncular parayı kazanacaklar (1 milyon doları cebe indirmek için tahminde bulunan iki kişinin de doğru tahminde bulunması gerekiyor.) Demek ki sadece bir kişinin pas geçmeyip tahminde bulunduğu strateji iki kişinin tahminde bulunma stratejisinden daha iyi, hatta iki katı daha iyi.
Herkes pas geçerse, kimse doğru tahminde bulunmadığından, kimse para kazanamayacak…
Bu n kişi odaya girmeden toplanıp en iyi strateji hakkında kafa yoruyorlar. En iyi stratejilerinin (varsa) en az % 50 olduğunu gördük. Yüzde elliden daha iyi bir strateji var mı?
Amerika’nın birçok ünlü matematikçisi, siz bu yazıyı okuduğunuz sırada belki de, bu konu üzerinde kafa yoruyor.
Oyunun kodlar teorisiyle ilgisi var, yani bilgisayarlarla, şifrelemeyle, bilgi yollamayla, yani çağımızın en çok kullanılan aygıtlarıyla… Matematik kimileyin de bir işe yarar!
Birçok matematikçi, problemi ilk duyduğunda en iyi stratejinin yukarıda açıkladığım, yüzde elli parayı kazandıran strateji olduğunu düşünüyormuş. Ama daha sonra daha iyi stratejilerin varlığını kavrıyorlarmış.
Problemi ilk kez Kaliforniya Üniversitesi’nden Dr. Todd Ebert doktorasını yazarken bulmuş. Soruyu öğrencilerine sormuş. Bir sabah uyandığında, internette herkesin bu problemle uğraştığını görmüş…
Yine Kaliforniya üniversitesinden Prof. Berlekamp n = 3 olduğunda, yüzde 75 kazandıran bir stratejinin olduğunu bulmuş. Biz de bulalım.
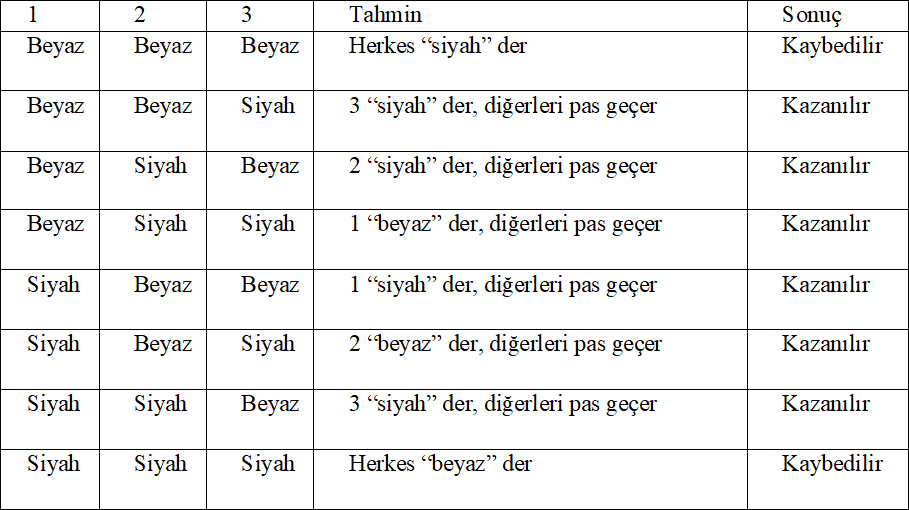
Şöyle düşünelim. Üç şapkanın üçünün de aynı renk olma olasılığı 1/4’tür, çünkü 1/8 olasılıkla üç şapka beyaz, 1/8 olasılıkla üç şapka siyah olacaktır. Dolayısıyla üç şapkanın renk dağılımının 2-1 olma olasılığı 3/4’tür. Demek ki, karşısındaki iki şapkanın aynı renkte olduğunu görenler aksi tahminde bulunurlarsa, yani iki siyah şapka gören beyaz, iki beyaz şapka gören siyah derse ve diğerleri pas geçerse, 3/4 olasılıkla doğru tahminde bulunulacaktır.
Bunu şöyle de gösterebiliriz. Oyunculara 1, 2, 3 diyelim ve bu stratejiyle oyunun akışına bakalım:
Eğer n = 15 ise, 15/16 olasılıkla kazandıran bir strateji bulunmuş.
Oyuncu sayısı arttıkça, bilinen bir stratejinin kazanma olasılığı artıyor, hatta n sonsuza gittiğinde bu bilinen stratejinin olasılığı 1’e yakınsıyormuş.
Biz Türkler bu oyunu biraz değiştirelim. Oyuncular –hep birlikte değil de– teker teker tahminde bulunsunlar. Bu oyunda en iyi strateji var mıdır, varsa bu en iyi stratejinin başarı şansı yüzde kaçtır?
Yukarıdaki gibi düşüneceğiz. Kişi sayısına n diyelim. Herkese siyah şapka gelme olasılığı 1/2n’dir, dolayısıyla en az bir kişiye beyaz şapka gelme olasılığı 1 – 1/2n’dir. Eğer en az bir kişiye beyaz şapka gelirse, oyunun –birazdan açıklayacağım stratejiyle– kazanılacağını iddia ediyorum.
Stratejim şu: Oyuncular sıraya dizilsinler: 1, 2, …, n ve bu sırayla tahminde bulunsunlar. Her oyuncu, kendisinden sonra gelen oyunculardan herhangi birinin başında beyaz şapka görmüyorsa (yani bütün şapkalar siyahsa), “beyaz” tahmininde bulunsun, eğer görüyorsa pas geçsin. Yani beyaz şapka görüldükçe pas geçilecek, görülmüyorsa “beyaz” denilecek… Daha sonraki oyuncular pas geçsinler…
Örneğin, 1 numaralı oyuncu eğer hiç kimsede beyaz şapka görmüyorsa, yani herkeste siyah şapka görüyorsa “beyaz” der (diğerleri pas geçer), eğer en az bir kişide beyaz şapka görüyorsa pas geçer (ve sıra ikinci oyuncuya geçer.)
Birinci oyuncu pas geçmişse, o zaman en az bir kişide beyaz şapka var demektir. En sonuncu beyaz şapka sahibi, kendisinden sonra beyaz şapka görmediğinden, tahminde bulunacak (daha öncekiler pas geçmiş olmalılar, daha sonrakiler de pas geçecekler) ve oyun kazanılacak.
Üç oyuncuyla neler olduğuna bakalım. Şapka dağılımlarını BBB, BBS,… gibi gösterelim. Örneğin BSB, birinci ve üçüncü oyuncularda beyaz, ikinci oyuncuda siyah şapka olduğunu gösteriyor.
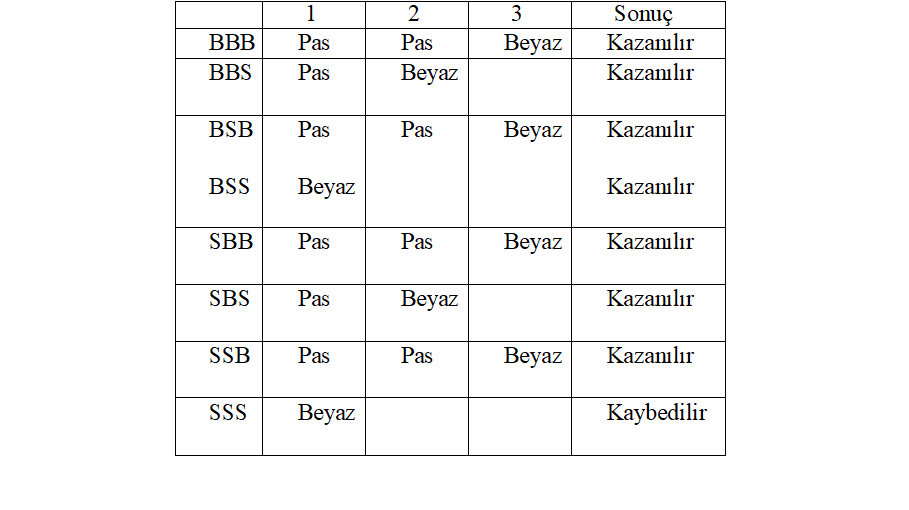
Görüldüğü gibi 7/8 olasılıkla oyun kazanılıyor.
Genel olarak n kişi varsa oyunda, en sonuncu beyaz doğru tahminde bulunacağından, oyun 1 – 1/2n olasılıkla kazanılır.
Daha iyi bir strateji de olamaz çünkü birinci kişi tahminde bulunduğunda en az 1/2n olasılıkla oyun kaybedilecektir, demek ki yukarıda açıklamaya çalıştığım stratejiden daha iyi bir stratejide, birinci oyuncu hep pas geçmelidir. Birinci oyuncu hep pas geçtiğinde de bir sonraki oyuncuya hiçbir ipucu vermeyecektir, dolayısıyla ikinci oyuncuyla birinci oyuncu arasında bir fark kalmayacaktır ve ikinci oyuncu da pas geçmek zorunda kalacaktır… Bu böyle devam eder.
Yazar: Ali Nesin (tümünü gör)
- Matematik ve Doğa - 18 Aralık 2019
- Loto! - 25 Eylül 2019
- Cemal Amca’nın Zarları - 29 Ağustos 2019
- Şapka Problemi - 15 Ağustos 2019
- Çok Basit Aritmetiğe Çok Basit Bir Çözüm - 1 Ağustos 2019




