Karl Weierstrass, Johann Sebastian Bach ve Neşe Karaböcek bir gün yürüyüşe çıkar…

Karl Weierstrass, bayağı üretken bir matematikçi. Matematikte çok sayıda temel teoremi var. Sadece bulduğu şeylerin listesi ve bir cümlelik özetleri bile, belki bu yazıdan daha uzun tutar. Bu yazımda, bir iddia sonucu bulduğu ilginç bir fonksiyondan bahsedeceğim. Ayrıca Bach ve Neşe Karaböcek’ten de bahsedeceğim (Ha? Efendim?)

Weierstass, süreklilik, türevlenebilirlik konusunda şirin bir fonksiyon önermiş. Çok teknik ayrıntılara girmezsek: sürekli demek, basitçe fonksiyonda bir kesinti olmaması demek. Mesela, sinüs fonksiyonu:

\(\sin(x) \)

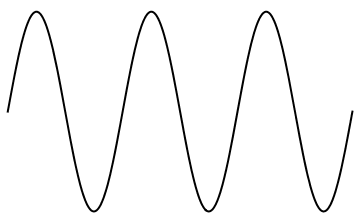
her \(x\) değeri için sürekli ve türevli, ama mesela şu eğri sürekli değil:

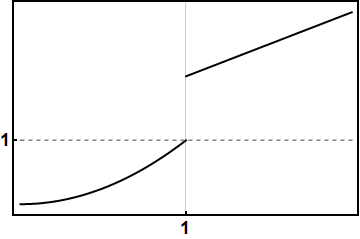
\(x = 1\)’e sağdan yaklaşırsanız başka bir sayıya, \(x = 1\)’e soldan yaklaşırsanız başka bir sayıya varıyorsunuz. Kesinti var, sıkıntı…

Türevlenebilir demek ise, basitçe bu fonksiyonun her yerde türevinin tanımlı olması demek. Tekrar, sinüs fonksiyonunun türevi her yerde tanımlı. Az önceki eğriyi biraz değiştirip sürekli yapsam bile \(x = 1\)’de türev tanımlı değil. \(x = 1\)’e sağdan yaklaşırsam eğim farkli, \(x = 1\)’e soldan yaklaşırsam eğim farkli.

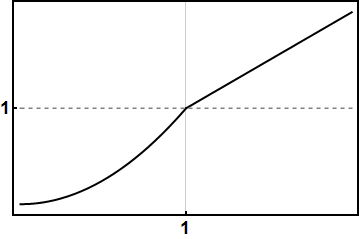
Weierstrass, bu “her yerde sürekli olan bir fonksiyon, aynı zamanda her yerde türevlenebilir mi?” sorusuna bir aksi-örnek vermiş. Şu karmaşık görünen fonksiyon,

\(f_a (x) = \displaystyle{\sum \limits_{k = 1}^{\infty} \frac{\sin(\pi k^a x)}{\pi k^a}}\)

her \(x\) noktasında sürekli, ama hiç bir \(x\) noktasında türevlenemiyor. Bu fonksiyonun başka bir özelliği de, kendi-benzer (self similar) olması. Yani, fraktal gibi, bir yeri büyüttüğünüz zaman yine benzer davranışı görüyorsunuz. Fraktaller ve Mandelbrot konusunda şu linkte daha ayrıntılı yazmıştım: Tik tik.

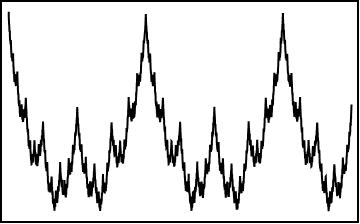
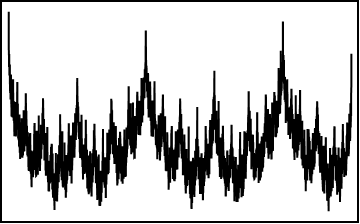
Şimdi… Size Weierstrass fonksiyonunu görsellerle anlatmak yerine, sesle anlatmak istiyorum. Johann Sebastian Bach’ın 1 numaralı keman konçertosu birinci parçasını (BWV 1041, bu kodu arada BMW diye okuduğum oluyor ehi), Johann Sebastian Bach’ın ‘İyi Düzenlenmiş Klavye’sinden kitap 1, no 2 (BWV 847) ve Neşe Karaböcek’in Artık Sevmeyeceğim şarkısını kodladım. Neden Neşe Karaböcek derseniz, neden Bach değil derim. Neden Bach derseniz, neden Neşe Karaböcek değil derim. Canımı sıkmayın, paşa gönlüm öyle istedi. Ne güzel parçalar işte… Sorgulamayın (bilim sayfasında sorgulamayın diyen yazar).

Bu üç parçayı dört ayrı este bilgisayarda kodladım. İlk olarak, sesi tamamen sinüs eğrisi ile çıkardım, yani telefonu kaldırdığınız zaman gelen çevir sesi basit sinüs sesi. Türkiye’de, çevir sesi 450 Hz ve la notası 440 Hz. Yani enstrümanınızı akort yapmak isterseniz ve yaklaşık ses almak isterseniz, çevir sesini kullanabilirsiniz. İsveç’te çevir sesi tam 440 Hz, yani la sesi. ABD’de iki tane ses kullanılıyor; 350 Hz ve 440 Hz. İkinci olarak, sesi Fourier serisinde çıkardım. Fourier serisi hakkında daha fazla bilgi almak isterseniz, önceki yazıma bakabilirsiniz. Üçüncü olarak, Weierstrass fonksiyonunu kullanıp bu parçaları tekrar çıkardım. Son olarak, deneme yanılma yoluyla ördek sesine benzettiğim bir fonksiyonla çıkardım. Bu fonksiyon böyle bir şey oldu artık:

Bach, birinci keman konçertosu, birinci parça. BWV 1041

Önce, parçanın gerçeğini dinleyin, az sonra gelecek dijital felaketten önce kulaklarınız bir temizlensin. Los Angeles Filarmoni Orkestrası, Alfred Wallestein, 1953. Keman solisti: Jasha Heifetz (baklava gerçek ustaların elinden yenir).

Sinüs fonksiyonu ile:

Fourier serisi ile:

Weierstrass fonksiyonu ile:

“Bilgecan’ın ördek sesine benzettiği fonksiyon” ile:

Sonraki bölümlere geçmeden önce Jasha Heifetz’i tekrar dinleyin de, arındırın bir kulakları. Yeterince işkence gördüler buraya kadar.

Bach, İyi Düzenlenmiş Klavye, Kitap 1, No. 2. BWV 847 Praeludium (Prelüdçük)

Parçanın gerçeği, piyanoda Karl Richter. (Bach zamanında piyano yoktu, klavsen, klavikord, harpiskord için yazılmış bunlar zamanında ama idare ediverin artıkın). Bach, İyi Düzenlenmiş Klavye kitaplarını, klavyeli bir enstrümanı test etmek için (sound check) yazmıs.

Sinus fonksiyonu ile (iki el):

Fourier serisi ile (iki el):

Weierstrass fonksiyonu ile (iki el):

“Bilgecan’ın ördek sesine benzettiği fonksiyon” ile (iki el):

Sonraki bölümlere geçmeden önce, tekrar kulaklar temizlensin. Richter’in kaydına pls.

Neşe Karaböcek, Artık Sevmeyeceğim

Sinus fonksiyonu:

Fourier serisi:

Weierstrass fonksiyonu:

“Bilgecan’ın ördek sesine benzettiği fonksiyon” ile:

Yazı, görseller ve sesler: Bilgecan Dede.

Bir Arkadas’a tesekkurler.

The following two tabs change content below.

• Bilgi
• Son Yazıları

Bilgecan Dede

Hukuğa kafası basmadığından meslek okuluna gitti bu. Ondan sonra gâvur bir ustanın yanına çırak verdiler eli iş tutsun diye, çok şükür ustalığını kazanmış ondan, şimdi de usta olmuş çalışıyor. Eli yüzü düzgün biriyle de evermişler. Ben diyorum, “Bak ileride torun combalak olacak, gel bir şirkette işe başla.” Ama dinlemiyor ki, asi biraz bu.

Yazar: Bilgecan Dede (tümünü gör)

• Fourier Serisi yazısına ek: - 23 Aralık 2018
• Yapay zekâ yüzünden kaybolacak ve eklenecek iş sayıları, bir tabloda - 4 Nisan 2018
• 130 yıl sonra gelen adalet: Telefonun mucidi resmî olarak Antonio Meucci! - 18 Şubat 2018
• Denklem Yazmak - 6 Ocak 2018
• Temel Harmonikler ve Lissajous Eğrileri - 17 Aralık 2017