Hiç Kısalmadan Kısalan Yol

İki metrelik bir yol, hiç uzayıp kısalmadan, bir metrelik bir yola dönüşebilir mi? Bu yazıda yanıtın evet olduğunu göreceğiz. İki metrelik bir yol, hepimizin gözleri önünde, bir santimetre bile kısalmadan bir metrelik bir yola dönüşecek.

Her kenarı 1 metre olan aşağıdaki eşkenar üçgene bir göz atın önce.

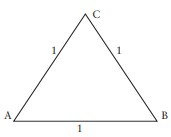
Bu üçgende A noktasıyla B noktası arasındaki uzaklık 1 metredir. Eğer A’dan B’ye gitmek için en kısa yol olan AB doğru parçasını seçecek olursak 1 metre gideriz. Ama A’dan B’ye gitmek için C’den geçecek olursak, yani ACB yolunu izlersek, 2 metre yol alırız, çünkü AC ve CB doğru parçaları birer metredir. ACB yolunu hiç kısaltmadan AB doğru parçasına dönüştüreceğim. Herkesin gözü önünde…

A’dan B’ye gitmek için yandaki zigzag yolu seçersek kaç metre gideriz?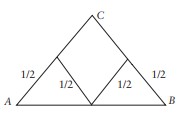

Dört kez yarım metre gideceğimizden, yolumuz gene 2 metre olur.

Ya aşağıdaki zigzagzigzag yolu izlersek?

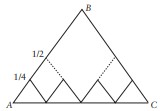
Gene iki metre gideriz, çünkü sekiz kez 1/4 metre yol katetmek zorunda kalırız.

Sağdaki yola bakalım: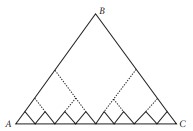

Bu yol da 2 metre, çünkü 16 kez 1/8 metre gidiyoruz.

Yollar gittikçe daha çok AB doğru parçasına yaklaşıyor, ama uzunlukları sabit (2 metre) kalıyor…

Görüldüğü gibi bu kırık yolların her birinin uzunluğu 2 metre.

Yukarıda yaptığımızı hiç durmadan (sonsuza dek) sürdürebiliriz, yani bu işlemin limitini alabiliriz. Kırık yollar “sonsuzda” AB doğru parçası olur. Matematiksel bir deyişle kırık yollar AB doğru parçasına yakınsar. Ama kırık yolların uzunluğu hep iki metredir. Her birinin uzunluğu iki metre olan yollar, nasıl olur da uzunluğu 1 metre olan bir yola yakınsayabilir? Yoksa 1, 2’ye mi eşittir? Değilse, ki değil, iki metrelik bir yol, nasıl oldu da hiç kısalmadan bir metrelik bir yola dönüştü?

Burada neler olup bittiğini açıklayabilir misiniz?

Açıklanacak bir şey yok!

Uzunluğu 2 metre olan yollar, uzunluğu 1 metre olan bir yola bal gibi de yakınsayabilir! Hepimizin gözleri önünde yakınsamadı mı?

Yolların limitinin uzunluğu (örneğimizde 1), o yolların uzunluklarının limitine (örneğimizde 2) eşit olmaya

bilir. Yukarıda olan da bu zaten.

Kırık yollara sırasıyla,

y₁, y₂, y₃, …

adlarını verelim. A’dan B’ye giden düz yola da y diyelim. Her y_n’nin uzunluğu 2 (çünkü y_n yolu, uzunluğu 1/2ⁿ olan 2ⁿ⁺¹ kırık yoldan oluşuyor), öte yandan y’nin uzunluğu 1. Bu y_n yolları sonsuzda y’ye yakınsar, bundan hiç kuşku yok. Ama y_n’lerin uzunlukları y’nin uzunluğuna yakınsamıyor.

Bu, her ne denli şaşılacak bir şeyse de matematikle çelişmiyor, herhangi bir “mantıksızlık” yok. Yukarıda olan biten çelişse çelişse sezgiyle çelişir.

Matematikte kimi zaman işte böyle şaşılası, sezgiyle pek anlaşılamayacak şeyler olur. Sezgiyle doğru olduğunu sandığımız, hatta doğruluğundan emin olduğumuz olguları, işte bu yüzden matematiksel olarak kanıtlamak zorunluluğunu duyumsarız. Sezginin yanıldığı olur. Yukarıda olduğu gibi.

Kimi okur yukarıda olanların nedenini şöyle açıklamış olabilir: “y_n yolları, kırık, köşeli yollardır.¹ O yollar yumuşak virajlı yollar olsalardı, böyle bir sorun olmazdı, y_n yollarının uzunluğu 1’e yakınsardı.” Bu açıklama doğru değildir. y_n yollarını biraz onarımla yumuşak virajlı yollara dönüştürebiliriz ve bunu öyle yapabiliriz ki, yumuşak virajlı yeni yollar gene AB doğrusuna yakınsar ama yolların hiçbirinin uzunluğu değişmez, gene 2 metredirler.

“Kusur” elbette kırık yollarda. Ama kırık yolların kırıklığında değil kusur. Biraz önce de dediğim gibi, kırık yolları yumuşak yollar haline getirsek bile sezgimizle çelişebiliriz (ama matematikle çelişmeyiz.) Bu yolların ne “kusuru” var?

Bu, bir popüler matematik yazısı olduğuna göre, y_n yollarının “kusurunu” herkesin anlayabileceği bir dilde açıklayabilmem gerekiyor. Ne yazık ki bu pek kolay olmayacak. Hatta başaramayacağımı daha başından biliyordum. Burada olan biteni tam anlamıyla anlayabilmek için matematik bölümünün en az ilk iki yılını bitirmek gerekir.

Tam açıklayamasam bile, sezgi gücümüzün matematikle yarışamayacağını gösteren güzel bir örnek bu bence.

Gene de açıklamaya çalışayım.

Evet… Yolların “kusuruna” geleyim. Yolların ne “kusuru” var?

İki çeşit kırık yolumuz var. Aşağıdaki doğru gibi yukarıya çıkanlar:

ve aşağıdaki doğru gibi aşağı inenler:

Birincisi gibi olanların eğimine 1/√3, ikincisi gibi olanların eğimine –1/√3 diyelim (denir!). Dileyen okur, bunları tanım olarak kabul edebilir. Her y_n yolu, eğimi 1/√3 ve –1/√3 olan doğru parçalarından oluşmuştur. Öte yandan y yatay bir yoldur ve eğimi 0’dır.

İlk koordinatı 1/3 olan ve y₁’in üstündeki noktaya bakalım. Bu nokta eğimi 1/√3 olan bir doğru parçasının üstündedir. (Aşağıdaki şekle bakın).

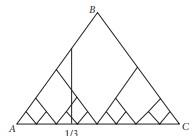İlk koordinatı 1/3 olan ve y₂’nin üstündeki noktaya bakalım. Bu nokta eğimi –1/√3 olan bir doğru parçasının üstündedir. (Gene yandaki şekle bakın.)

İlk koordinatı 1/3 olan ve y₃’ün üstündeki noktaya bakalım. Bu nokta eğimi 1/√3 olan bir doğru parçasının üstündedir.

İlk koordinatı 1/3 olan ve y₄’ün üstündeki noktaya bakalım. Bu nokta eğimi –1/√3 olan bir doğru parçasının üstündedir.

Bunu böyle sürdürebiliriz. Bir önceki 1/3 Nerde? Başlıklı yazımızı iyi anlayan okur, eğimlerin durmadan 1/√3 ve –1/√3 olarak değiştiğini görecektir. Öte yandan y’nin eğimi 0’dır.

İşte y_n’lerin kusuru bu: y_n’ler y’ye yakınsıyor ama y_n’lerin eğimleri y’nin eğimine yakınsamıyor. y_n’lerin eğimleri kâh 1/√3 kâh –1/√3 oluyor, ama y’nin eğimi 0.

Peki, ya y_n’lerin eğimi, y’nin eğimine yakınsasaydı? O zaman ne olurdu? O zaman da böyle bir sorun çıkabilirdi. Böyle bir sorun çıkmaması için, yani y_n’lerin uzunluklarının limitinin y_n’lerin limitinin uzunluğu olabilmesi için, y_n’lerin eğiminin y’nin eğimine yakınsamasından başka, bu yakınsamanın düzgün bir yakınsama² olması gerekirdi. “Düzgün yakınsama” konusunu, burada, böyle kısa bir popüler matematik yazısında açıklamaya kalkışmama yeteneklerim müsaade etmiyor…

Kaynak : Matematik ve Sonsuz

The following two tabs change content below.

• Bilgi
• Son Yazıları

Ali Nesin

Ali Nesin'in izniyle, yazılarını siteye eklemek için açılmış bir hesaptır. Okuduğunuz Ali Nesin yazılarına karşılık Nesin Vakfı'na bağışta bulunursanız seviniriz. Bu yazıları da içeren kitapları Nesin Yayınevi'nden elde edebilirsiniz.

Yazar: Ali Nesin (tümünü gör)

• Matematik ve Doğa - 18 Aralık 2019
• Loto! - 25 Eylül 2019
• Cemal Amca’nın Zarları - 29 Ağustos 2019
• Şapka Problemi - 15 Ağustos 2019
• Çok Basit Aritmetiğe Çok Basit Bir Çözüm - 1 Ağustos 2019