Ağırlıksız Ortam
Uzay İstasyonu’nda neden ağırlıksız olursunuz?
İlk önce, terazinin üzerine çıktığınızda gördüğünüz tam olarak nedir (eheh)? Dünya’nın kütlesinden dolayı, üzerinizde bir kütleçekim kuvveti var. Newton asırlar önce formüle etmiş bu kuvvetin temelde nasıl olduğunu. Terazinin üzerine çıkıyorsunuz, kütleçekim kuvveti ve yerin sizin üzerinize uyguladığı kuvvet birbirine eşit olduğundan terazinin üzerinde durabiliyorsunuz. Terazi de kendisine uygulanan kuvveti size söylüyor [3]. Böylece ağırlığınızı ölçebiliyorsunuz.
Teraziyi halı üzerine koyup tekrar tartılırsanız, sizin ağırlığınızdan daha düşük gösterecektir. Çünkü, halı biraz esnedi ve teraziye uygulanan kuvvet sadece ağırlığınıza eşit değil; artık ağırlığınızdan halının küçük esneme kuvvetini çıkardınız. Teraziyi, yay sabitini bildiğiniz dört yay üzerine koyup, dört yayı sert bir yüzey üzerine koyarsanız ve tartılırsanız bu etkiyi ölçebilirsiniz.
Şimdi terazi ile bir uçağa bindiniz ve uçaktan atladınız. Havada iken terazi ile tartılmaya çalışıyorsunuz (çünkü manyaksınız). Hava olmasın, çünkü havanın direnç kuvveti ile uğraşmak istemiyorum. Terazi tabi ki de sıfır ölçecektir. Sebebi, terazi ile sizin eylemsiz olmanız. İkiniz de aynı ivmeye sahipsiniz. Terazinin ölçtüğü bir kuvvet yok. İkinize de etki eden sadece bir kuvvet var, o da yerçekimi (ya da kütleçekim) kuvveti.
Eylemsiz sistemde olduğunda bir kuvvet hissetmezsiniz [1]. Uçak sabit hızda giderken önünüzdeki masaya bir telefon koyun, telefon orada hareketsiz kalacaktır [1]. Çünkü siz ve telefon uçak içerisinde eylemsizsiniz. Uçak bir kalkış yaptığında, telefon geriye hareket edecek, çünkü ivme yapıyor ve artık eylemsiz değil [2]. Bu sebeple bazı kaynaklarda kütle, “eylemsizlik” (inertia) olarak geçer. Kütlenin zilyon tane tanımından Newton’a göre olanı: “hareket etmekten ne kadar nefret ediyorsunuz” (başka bir deyişle, tembellik yasası) [4].
Elimizde bunlar varken, Uluslararası Uzay İstasyonu’nda (UUİ) çalışan astronotlar neden ağırlıksızdır? Yerçekimi çok mu az? Bir duvardan itibaren on adım atın. Duvar Dünya’nın yüzeyi, onuncu adımın bittiği yer Ay olsun, yani Dünya Ay arasındaki ortalama mesafeyi on adıma indirdiniz. UUİ’nin yörünge çizdiği ortalama mesafe duvardan itibaren işaret parmağınızın beşte biri. Yani yerçekimi çok değişmiyor. Sayısal olarak yerçekimi, ortalama yerçekim ivmesinin %89’u.
Astronotlara etki eden tek kuvvet halen kütleçekim kuvveti. Başka bir net kuvvet yok, yani “merkezkaç” kuvveti yok. Merkezkaç kuvvetini bir ipe top bağlayıp çevirirseniz, gerilme kuvvetinde hissedebilirsiniz. Ancak UUİ’de böyle bir gerilme kuvveti vs. söz konusu değil. Sadece kütleçekim kuvveti var ve buna bağlı olarak astronotlar aslında sürekli olarak serbest düşme halindeler. UUİ ve astronotlar eylemsiz, aynı ıvmede düşüyorlar ve haliyle ağırlık hissetmiyorlar. Peki sürekli astronotlar ve UUİ serbest düşme halindeyse UUİ neden hiç düşmüyor?
UUİ’nin çok yüksek bir yatay hızı var. Dünya’nın çevresinde yaklaşık doksan dakikada bir yörünge tamamlıyor. Eğer bu hızdan dolayı oluşan merkezcil kuvvet, yerçekimi kuvvetine eşitse, UUİ’nin düştüğü mesafe kadar, Dünya’nın yüzeyi de eğri olduğundan, aynı oranda alçalacak [5].
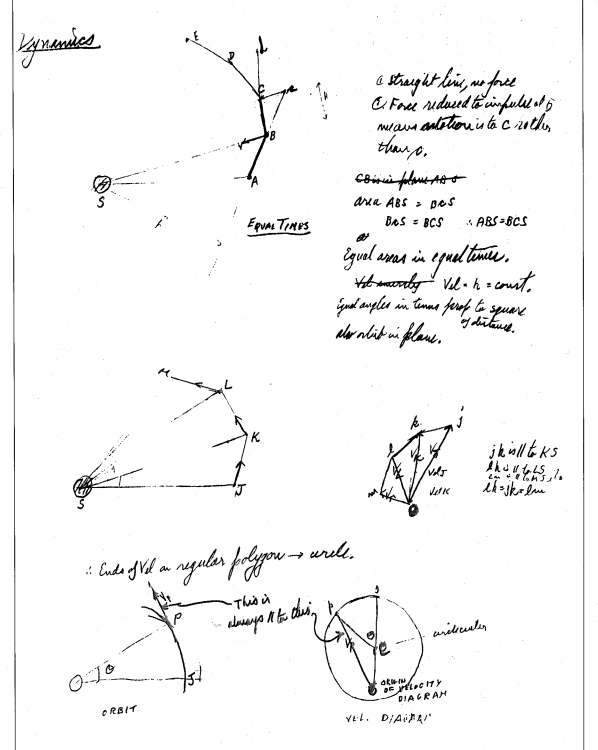
Dünya düz olsun. Siz de UUİ içindesiniz ve yine aynı hızınız var. Yine aynı şekilde serbest düşme halinde olursunuz ve ağırlık hissetmezsiniz. Ancak, yatay hızdan dolayı, düz olan Dünya üzerine eninde sonunda düşersiniz. Dünya yuvarlak olduğundan, eğer merkezcil kuvvetiniz yerçekimi kuvvetine eşitse Dünya’ya asla düşmezsiniz. Merkezcil kuvvetiniz eğer yerçekimi kuvvetinden daha düşük ise, heh, hapı yuttunuz. Düştüğünüz mesafe Dünya’nın eğriliğinden dolayı değiştiği yükseklikten daha fazla ve eninde sonunda Dünya yüzeyine düştünüz. Geçmiş olsun.
Son paragraftaki tartışmayı, “efektif yerçekimi ivmesi” şeklinde daha pratik şekilde yazabiliriz. Yerçekimi kuvvetinden merkezcil kuvveti çıkardığınızda sizin ağırlığınızı buldunuz. Bu, UUİ’de ölçtüğünüz ağırlık, eğer bir baskül götürüp altınıza koyarsanız baskülde bu farkı ölçeceksiniz. Ancak, bu iki kuvvet arasındaki farkı unutmamak lazım. Yerçekimi kuvveti her türlü var. Hareket etseniz de var, hareket etmeseniz de. Merkezcil kuvvet ise sadece dairesel hareket yaparsanız var. Dairesel hareket yapmazsanız, sadece kütleçekim altında olursanız yine ağırlık hissetmezsiniz.
UUİ’nin yükseğe koyulmasının sebebi de, bu yükseklikte hava direncinin çok az olması ve bu yüksek hızı korumak için daha az enerji sarf etmek gerekmesi. Ancak, hava direnci tamamen yok değil. Atmosferin yoğunluğu aniden değişmiyor, sürekli olarak değişiyor. Bu küçük hava direnci yüzünden, UUİ çok yavaş bir oran ile hız kaybediyor ve bu yüzden tekrar irtifa kazanması gerekiyor. Heh, tam bu anda motorlar çalıştığı zaman işin içine bir ivme giriyor, astronotlar artık eylemsiz olmuyorlar ve bu ivmeyi gözlemleyebiliyorlar. Bu videoda irtifa kazanma anındaki ivme gösteriliyor.
[1,2,3] Newton’un birinci [1], ikinci [2], üçüncü [3] yasası.
[4] Kütlenin bu tanımının, yerçekiminden ölçülen kütleye eşit olması bariz gibi görünür, ancak bu eşitliğin altında daha büyük bir fikir vardır. O da genel görelilik. Bu fikir genel göreliliğin dayandığı kurallardan biridir. O da artık başka bir yazımıza…
Soru: (Sürtünmeyi ihmal edersek) UUİ, Dünya çevresinde dairesel yörünge izlerken aşağı düşüp, hızı artıp eliptik yörüngeye oturmaz mı?
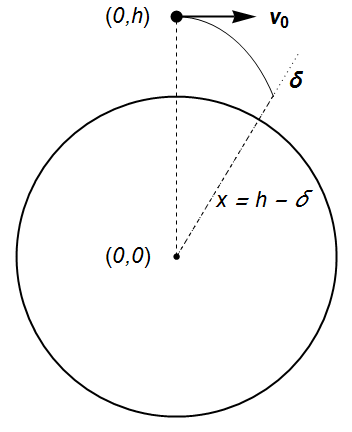
Cevap: Hayır. Bu Newton’un topu problemi. İnternette Newton’un problemi hakkında yeterince kaynak bulabilirsiniz. Tekrar etmek istemiyorum. Ben burada başka bir şekilde göstereceğim. Başlangıçta cismin (UUİ) sadece yatay (teğet) hızı olsun:
\({\bf v}_0 = v_0 \hat{\bf e}_x\)
Başlangıçtaki konumu (Dünya’nın merkezine göre):
\({\bf r}_i = \left(0, h \right)\)
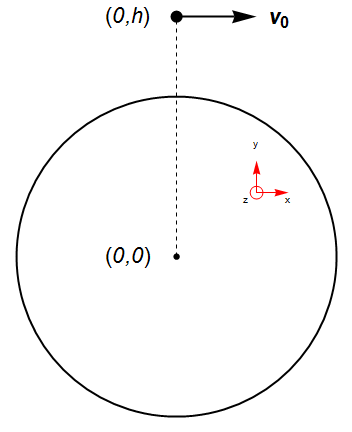
Cisim \(\Delta t\) kadar zaman sonra konumu (Dünya’nın merkezine göre):
\({\bf r}_f = \left(v_0 \Delta t, h + \Delta y\right)\).
Yörünge dairesel ise yapılan iş,
\(W = \displaystyle{\int {\bf F} \cdot d{\bf r}} = \Delta K = \displaystyle{K_f }- \displaystyle{K_0},\)
\(K = (1/2)m v^2\) ananemizin kullandığı kinetik enerji. Dünya ve cisim arasındaki kütlecekim kuvveti;
\(\displaystyle{{\bf F} = -\frac{GmM_D}{r^2}\hat{\bf r} \equiv -\frac{k}{r^2} \hat{\bf r} }.\)
Cisim Dünya etrafında döndükçe pozisyonu şöyle değişir;
\(d{\bf r} = r d\theta \pmb{\hat \theta} + \underbrace{dr \hat{\bf r}}_{0}\)
\(\pmb{\hat \theta} \perp \hat{\bf r}\) oldugundan, \(W=0\). Yani \(v_f = v_0\), tabi ki hiz degismez.
Pekala, \(\Delta t\) kadar zaman sonra cismin konumu nedir?
\({\bf r}_f = \left(x \sin\theta, x \cos\theta\right)\)
Önceki konum ile karşılaştırarak ilk sonucu bulurum:
\(v_0 \Delta t = x \sin\theta \rightarrow \Delta t = \displaystyle{\frac{x \sin\theta}{v_0}}\)
Önce, daha az karakter girmek için şöyle bir basitleştirme yapıyorum; \(F = |{\bf F}|\) ve \(a_0 = F/m\) (yani ivme). Şimdi de diğer \(y\) konumuna girişeyim.
\(\Delta y = \displaystyle{-\frac{1}{2}a_0 (\Delta t)^2}\)
\(h + \Delta y = x \cos\theta = h – \frac{1}{2}a_0 (\Delta t)^2\)
Yukarıdan \(\Delta t\)’yi yerine yazıyorum:
\(x^2 \displaystyle{\left(\frac{a_0 \sin^2\theta}{2 v_0^2}\right)} + x \displaystyle{\cos\theta }- \displaystyle{h} = 0\)
Şimdi bu bulduğum sonucu çözeceğim.
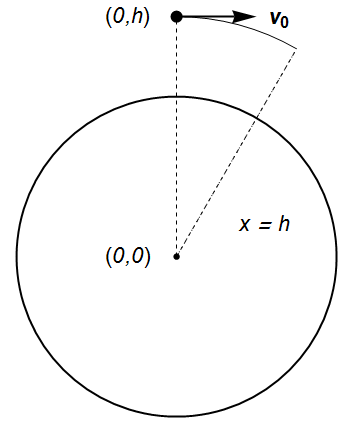
1) Dairesel yörünge ise \(x = h\)
\(h^2 \displaystyle{\left(\frac{a_0 \sin^2\theta}{2 v_0^2}\right)} + h \displaystyle{\cos\theta }- \displaystyle{h} = 0\)
\(h = \displaystyle{\frac{(1-\cos\theta)}{a_0 \sin^2\theta} 2 v_0^2} \rightarrow \displaystyle{\frac{v_0^2}{h}= a_0 \left(\frac{\sin^2\theta}{2(1-\cos\theta)}\right) }\)
Anlık hızla ilgilendiğimizden \(\theta \approx 0\).
\(\displaystyle{\lim_{\theta \rightarrow 0 }\left(\frac{\sin^2\theta}{2(1-\cos\theta)}\right)} = 1\)
Böylece,
\(\displaystyle{\frac{v_0^2}{h}}= \displaystyle{a_0 }=\displaystyle{\frac{F}{m}}\),
\(\displaystyle{m\frac{v_0^2}{h}}= \displaystyle{F}\),
Yani, dairesel yörünge için koşul, merkezcil kuvvetin kütlecekim kuvvetine eşit olması!
2) Eliptik yörünge, \(x = h + \delta\)
\(v_0^2 = a_0 \displaystyle{\frac{(h+\delta)^2 \sin^2\theta}{2(h-(h+\delta)\cos\theta)}}\)
Bunu şu şekilde yazabilirim (\(\epsilon = \delta/h\)):
\(\displaystyle{\frac{v_0^2}{h}} – \displaystyle{a_0} = a_0 \left[\underbrace{\displaystyle{\frac{(1+\epsilon)^2\sin^2\theta}{2(1-(1+\epsilon)\cos\theta)}}}_{>1}-1\right]\).
İşaretlediğim yer, \(\theta \rightarrow 0\) limitinde ve \(\epsilon > 0\) için her zaman 1’den büyük. Yani,
\(\displaystyle{\frac{v_0^2}{h}} – a_0 > 0\),
\(\displaystyle{m\frac{v_0^2}{h}} > F \),
Demek oluyor ki, eliptik yörünge izlemek için koşul merkezcil ıvme kütlecekim kuvvetinden fazla olacak.
3) Eliptik yörünge, \(x = \displaystyle{h} -\displaystyle{ \delta}\)
\(v_0^2 = a_0 \displaystyle{\frac{(h-\delta)^2 \sin^2\theta}{2(h-(h-\delta)\cos\theta)}}\)
Ayni hikaye (\(\epsilon = \delta/h\)):
\(\displaystyle{\frac{v_0^2}{h}} – \displaystyle{a_0} = a_0 \left[\underbrace{\displaystyle{\frac{(1-\epsilon)^2\sin^2\theta}{2(1-(1-\epsilon)\cos\theta)}}}_{<1}-1\right]\).
Şimdi de işaretlediğim yer, \(\theta \rightarrow 0\) limitinde ve \(\epsilon > 0\) için her zaman 1’den küçük.
\(\displaystyle{\frac{v_0^2}{h}} – a_0 < 0\),
\(\displaystyle{m\frac{v_0^2}{h}} < F \)
Yani, eğer merkezcil kuvvet kütlecekim kuvvetinden düşükse cisim düşebilir.
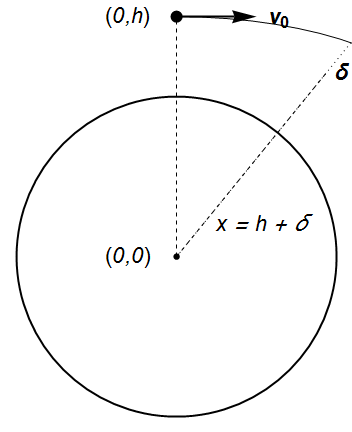
İkinci maddedeki durum, kapalı eliptik yörünge olabilir. Hangi koşullar altında olabilir bu eliptik yörünge? Bunun için önce cismin enerjisini yazıyorum (Dünya’nın göreli konumunda):
\(E = T + U = K_r + K_{\theta} + U = \displaystyle{\frac{1}{2}m \dot{r}^2} + \displaystyle{\frac{1}{2}m r^2 \dot{\theta}^2} – \displaystyle{\frac{k}{r}}\)
Kuvvet korunumlu olduğundan (\({\mathbf \nabla} \times {\bf F} = 0\)) hemen bir Legendre dönüşümü ile Lagrangıan’ı yazabilirim \(L = \displaystyle{T} -\displaystyle{ U}\):
\(S = S_r(r) + S_{\theta}(\theta) – E \, T = \displaystyle{\int_{t_0}^{t_f} L dt}\).
\(t_0\) ve \(t_f\)’de \(\delta r=0\) ise (uzun lafın kısası),
\(\displaystyle{\frac{\partial S}{\partial r} }= \displaystyle{\frac{\partial L}{\partial \dot{r}} } = p_r = m \dot{r}\)
ve
\(\displaystyle{\frac{\partial S}{\partial \theta} }= \displaystyle{\frac{\partial L}{\partial \dot{\theta}} } = p_{\theta} = m r^2\dot{\theta}\),
\(H = \displaystyle{\frac{p_r^2}{2m}} + \displaystyle{\frac{p_{\theta}^2}{2 m r^2}} – \displaystyle{\frac{k}{r}}\).
Pekala, simdi kuvveti yazıyorum:
\({\bf F} = \displaystyle{\frac{\Delta {\bf p}}{\Delta t}}\)
\(-\displaystyle{\frac{k}{r^2}}{\bf \hat{r}} = \displaystyle{\frac{\Delta p_r}{\Delta t}} {\bf \hat{r}} + \underbrace{\displaystyle{\frac{\Delta p_{\theta}}{\Delta t}} {\bf \hat{z}}}_{=0}\)
Kuvvet merkezcil olduğundan açısal momentum korunur,
\(-\displaystyle{\frac{k}{r^2}} = \displaystyle{\frac{\Delta p_r}{\Delta t}} \)
Ama radyal momentum korunmaz… Bu sonuç ile biraz oynayayım:
\(\Delta p_r = -\displaystyle{\frac{k}{r^2}}\Delta t\)
\(\Delta p_r = -\displaystyle{\frac{k}{p_{\theta}}}m \displaystyle{\frac{\Delta \theta}{\Delta t}}\Delta t = -\displaystyle{\frac{k}{p_{\theta}}}m \Delta \theta\)
\(\Delta p_r = m \Delta \dot{r}\) oldugundan, \(|\Delta \dot{r}| =\underbrace{\displaystyle{\frac{k}{p_{\theta}}}}_{sabit!} \Delta \theta \rightarrow\) Feynman’ın kayıp dersindeki sonucun aynısı! Yani, eliptik yörüngede, eşit acılar için radyal hız değişimi sabit!
Göstermek istediğim (daha doğrusu oynamak istediğim eheh) son bir sonuç var. Eğer toplam enerji (Dünya referans sisteminde) \(E < 0\) ise ve açısal momentum sabit ise,
\(-|E| = \displaystyle{\frac{p_r^2}{2m}} + \displaystyle{\frac{p_{\theta}^2}{2 m r^2}} – \displaystyle{\frac{k}{r}} \)
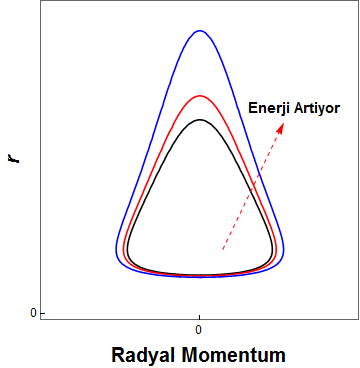
Momentum (\(p_r\)) – uzaklik (\(r\)) grafigi. Acisal momentum (\(p_{\theta}\)) sabit. Siyah, kirmizi, mavi egrilere dogru toplam enerji artiyor.
Bu sonuç kapalı bir yörüngeyi tanımlıyor.
Yazar: Bilgecan Dede.
Doga Kurkcuoglu
Yazar: Doga Kurkcuoglu (tümünü gör)
- Fourier Serisi yazısına ek: - 23 Aralık 2018
- Yapay zekâ yüzünden kaybolacak ve eklenecek iş sayıları, bir tabloda - 4 Nisan 2018
- 130 yıl sonra gelen adalet: Telefonun mucidi resmî olarak Antonio Meucci! - 18 Şubat 2018
- Denklem Yazmak - 6 Ocak 2018
- Temel Harmonikler ve Lissajous Eğrileri - 17 Aralık 2017




