Salı, Kasım 19, 2024
Latest:
Bilim Ne Güzel Lan
Cebir Fizik 

Fuyye Serisi ve Görüntüden Ses Çıkarmak

Bilgecan Dede 50 Comments , , , ,

Fourier serisi, tekrar eden bir eğriyi sinüs eğrilerinin toplamı olarak ifade etmektir. Sinüs dalgalarının toplamı şeklinde yazmanın diğer anlamı “hangi frekanstaki dalgadan ne kadar var” anlamına geldiğinden mühendislikte, fizikte, matematikte çok yaygın kullanılır. Altında yatan temel fikir, sinüs ve kosinüs fonksiyonlarının birbirine dik olmasıdır, sanki birbirlerine dik vektörler gibi.

\(\displaystyle{\frac{1}{\pi}\int \limits_{-\pi}^{\pi} {\color{black}\sin({\color{red}n} x)}{\color{black} \sin({\color{blue}m} x)} dx = \begin{cases} 1, & {\color{red}n} = {\color{blue}m} \\ 0, & {\color{red}n} \neq {\color{blue}m}\end{cases}}\)

\(\displaystyle{\frac{1}{\pi}\int \limits_{-\pi}^{\pi} {\color{black}\cos({\color{red}n} x)}{\color{black} \cos({\color{blue}m} x)} dx = \begin{cases} 1, & {\color{red}n} = {\color{blue}m} \\ 0, & {\color{red}n} \neq {\color{blue}m}\end{cases}}\)

\(\displaystyle{\frac{1}{\pi}\int \limits_{-\pi}^{\pi} {\color{red}\sin({\color{red}n} x)}{\color{blue} \cos({\color{blue}m} x)} dx =0}\)

Hatırlatma, iki birim vektör birbirine dik ise aynı sonucu verecekler.

\({\bf \hat{{\color{red}e}}}_{\color{red}i} \cdot {\bf \hat{{\color{blue}e}}}_{\color{blue}j} = \begin{cases} 1, & {\color{red}i} ={\color{blue} j} \\ 0,&  {\color{red}i} \neq {\color{blue}j} \end{cases}\)

Joseph Fourier

Bu sonucu ilk Euler fark ettiği halde, Fourier bunun önemini anlayıp dalgaların analizinde çok önemli olduğunu gösterdiğinden onun ismi ile anılır. Tanımı (daha bir çok formu var, bu Fourier’in bulduğu şekli);

\(\displaystyle{f(x) = \frac{a_0}{2} + \sum \limits_{n = 1}^N \left[ a_n {\color{red} \sin(n x)} + b_n {\color{blue}\cos(nx)}\right]},\)

\(f(x)\) seriye açmaya çalıştığımız periyodik bir fonksiyon \(x \in [-\pi, \pi]\), \(a_0\) bir sabit,

\(a_0 = \displaystyle{\frac{1}{\pi} \int \limits_{-\pi}^{\pi} f(x) dx }\)

ve \(a_n\) ve \(b_n\) şöyle tanımlanmışlar:

\(a_n = \displaystyle{\frac{1}{\pi} \int \limits_{-\pi}^{\pi} f(x) {\color{blue} \cos(nx) }dx },\)

\(b_n = \displaystyle{\frac{1}{\pi} \int \limits_{-\pi}^{\pi} f(x) {\color{red}\sin(nx) }dx }.\)

Bir kaç basit fonksiyonun Fourier dönüşümünü göstermek istiyorum. Çünkü çok eğlenceli (ᵔᴥᵔ)

İlk fonksiyonumuz +1 ile -1 arasında gidip gelen sinyal:

+1 ve -1 arasında gidip gelen basit sinyal. Bunu şimdi sinüslerin toplamı şeklinde yazmaya çalışacağız. Ne kadar çok terim eklersek o kadar iyi.

Bunu şimdi Fourier serisi şeklinde yazmaya çalışıyoruz. Her bir sinüs eğrisinin sadece bir frekansı var. Hangi frekanslardan ne kadar var onu bulmaya çalışıyoruz. Fourier serisinin sonucunu yazıyorum:

\(f(x) = \displaystyle{ \sum \limits_{n = 1,3,5,7…}^{\infty} \left(\frac{4}{n \pi}\right)\sin\left(\frac{n \pi x}{L}\right)}\)

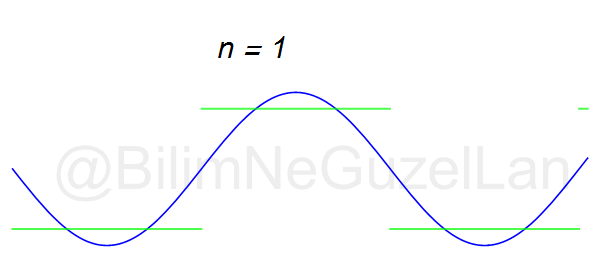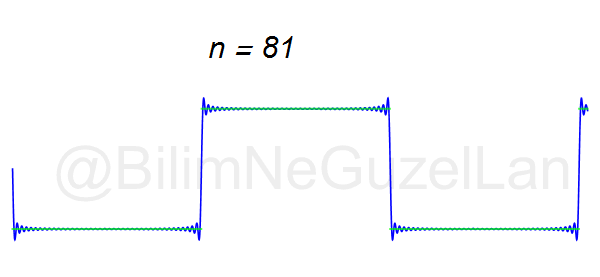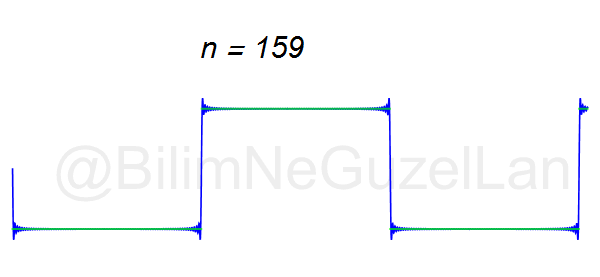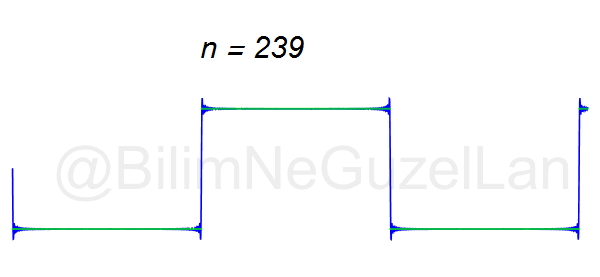
\(L\), bu \(f(x)\)’in periyodu, bu örnek için \(2\pi\). Aşağıdaki animasyonlarda \(n = 1\)’den \(n = 3,5,7,9,11,13,15\)’e kadar terimleri alarak Fourier serisini göstereceğim.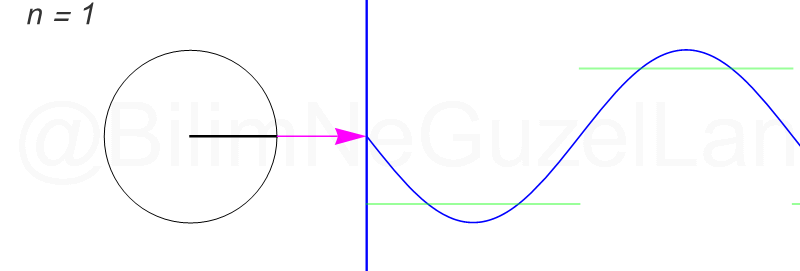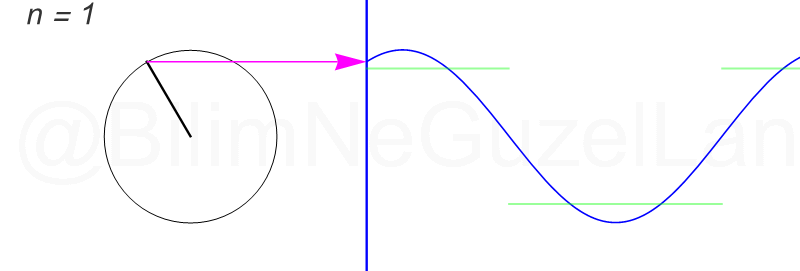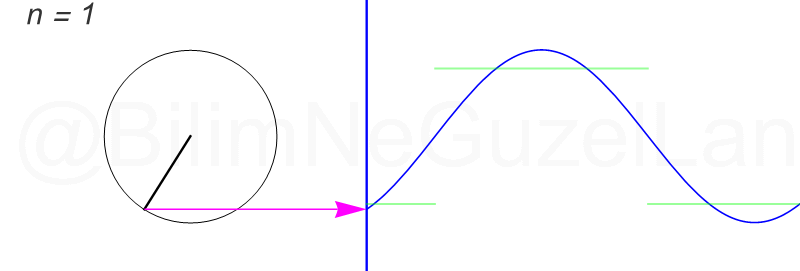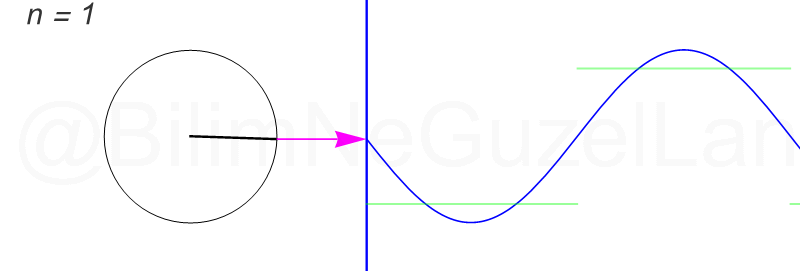 

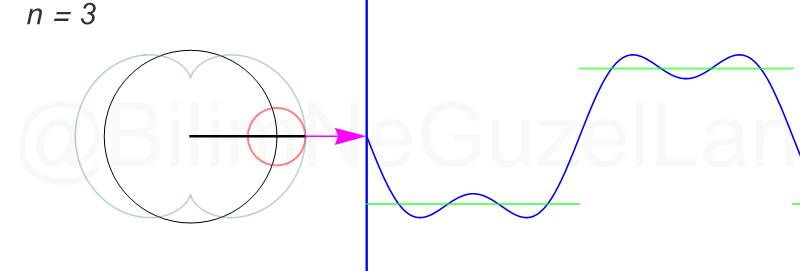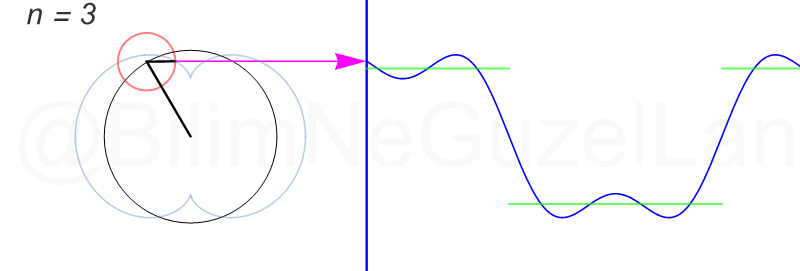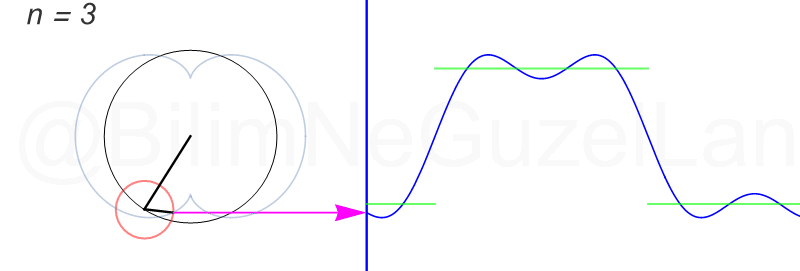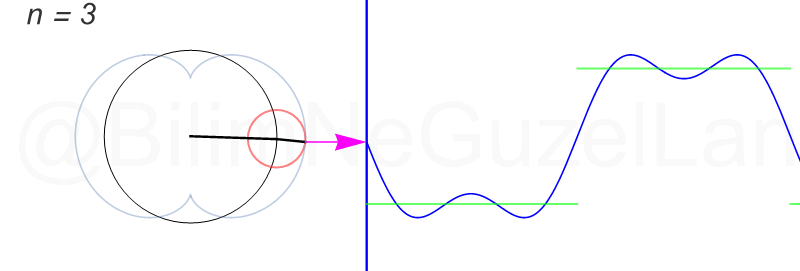
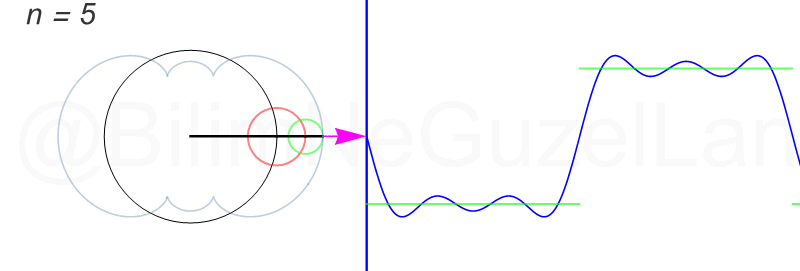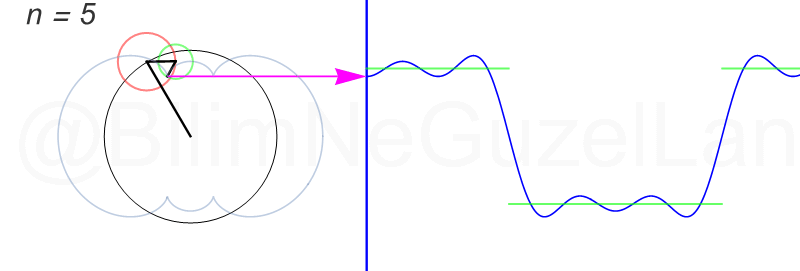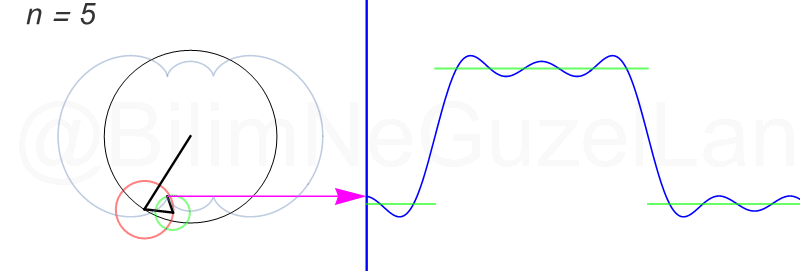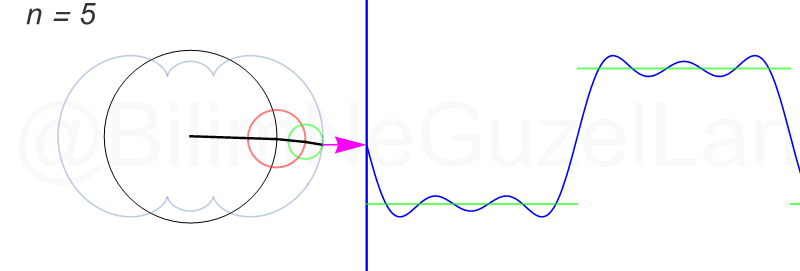
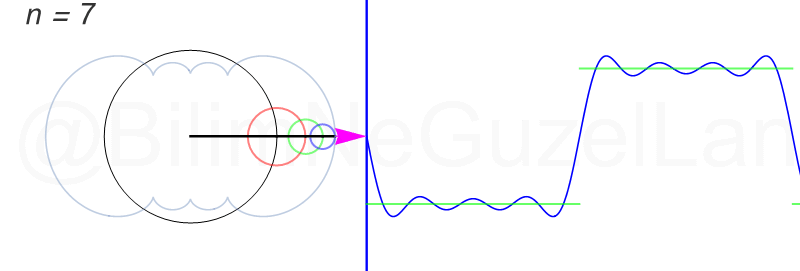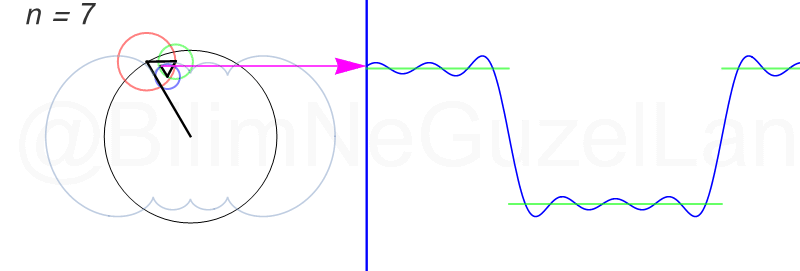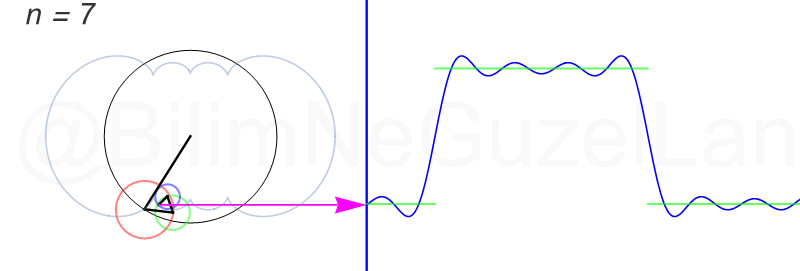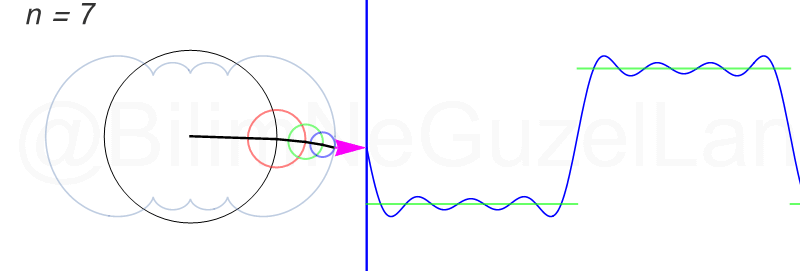
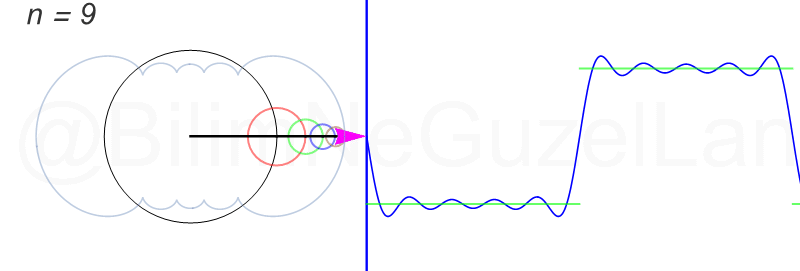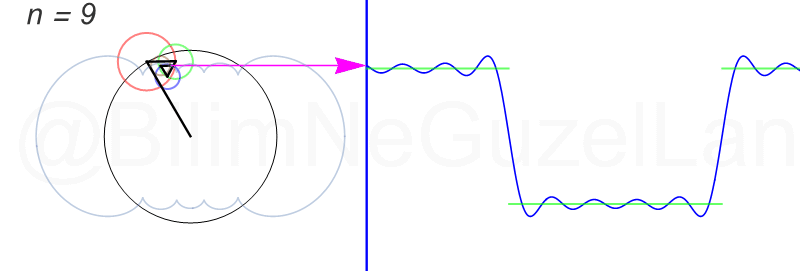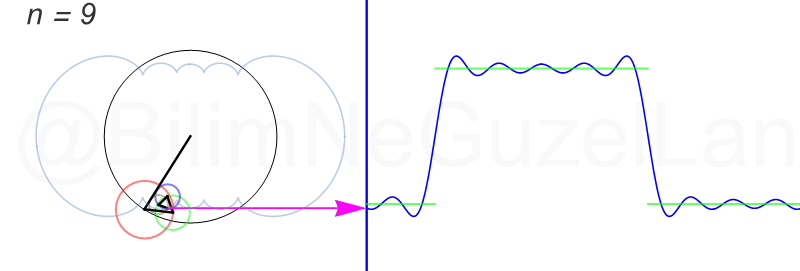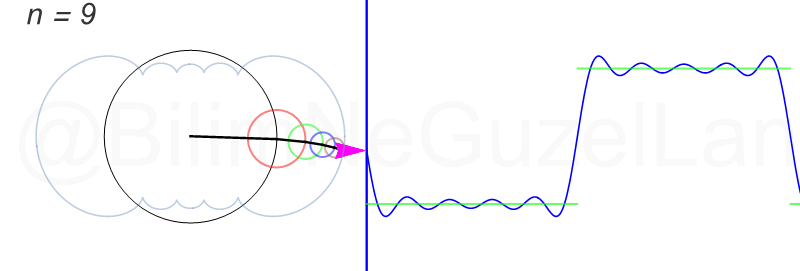
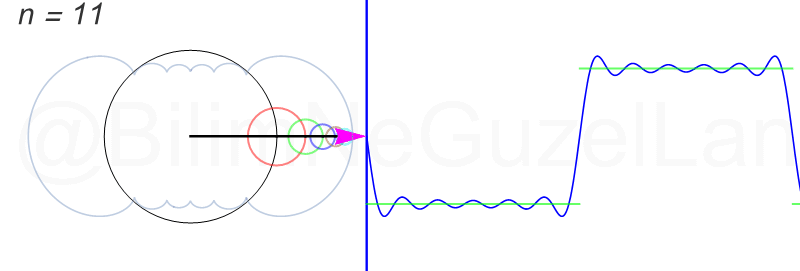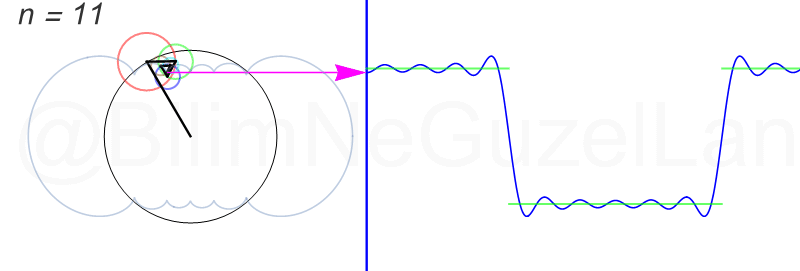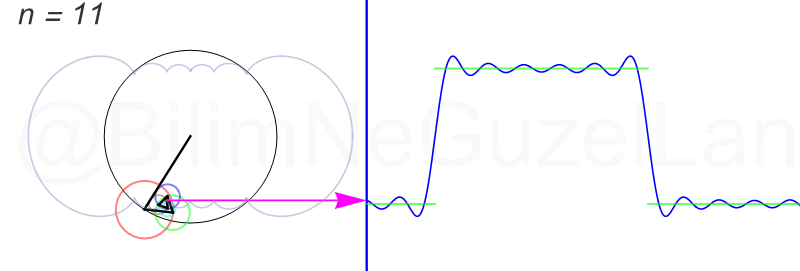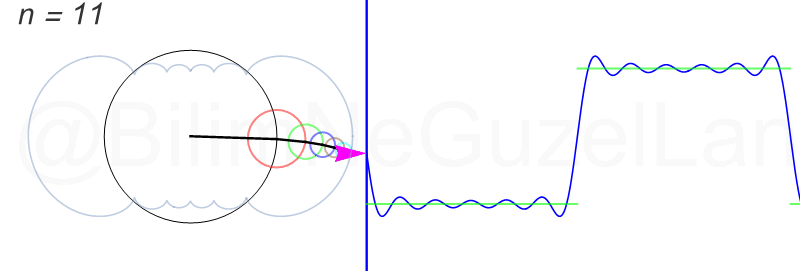
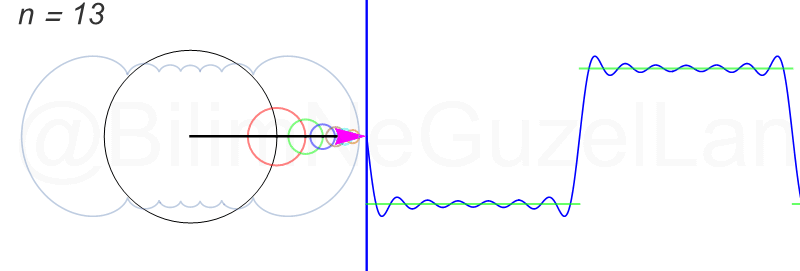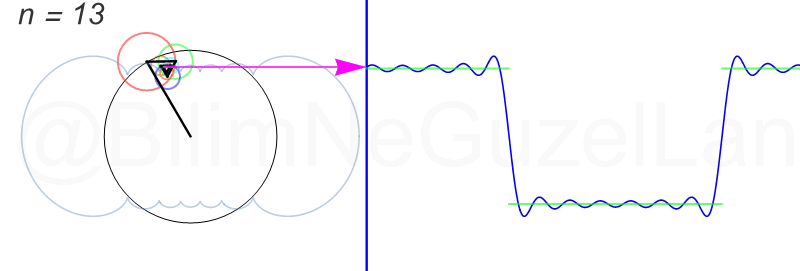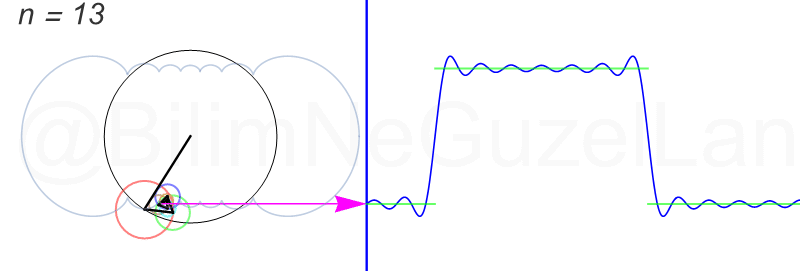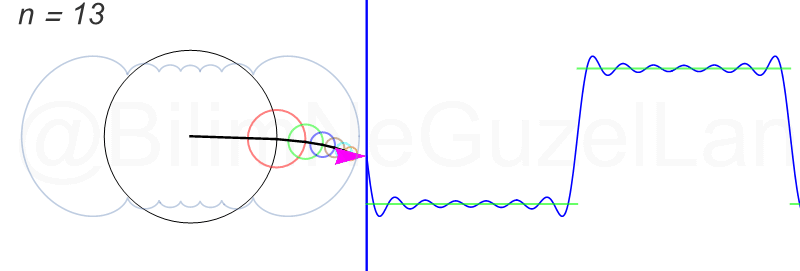
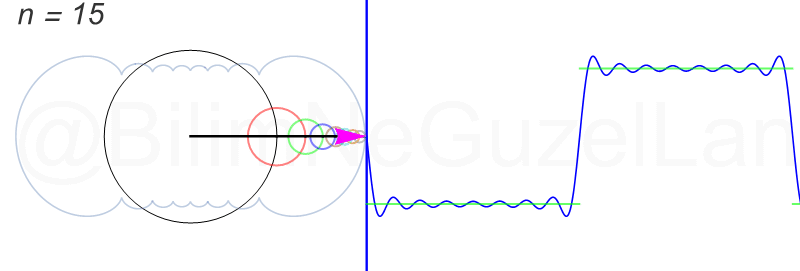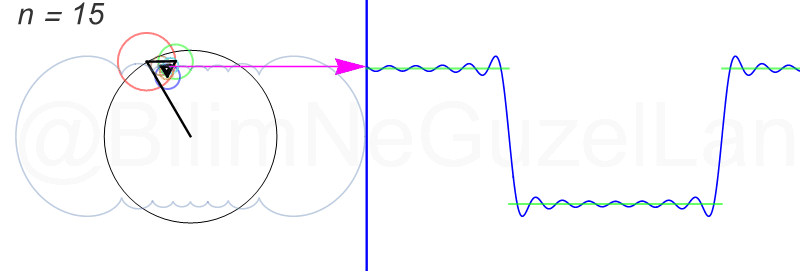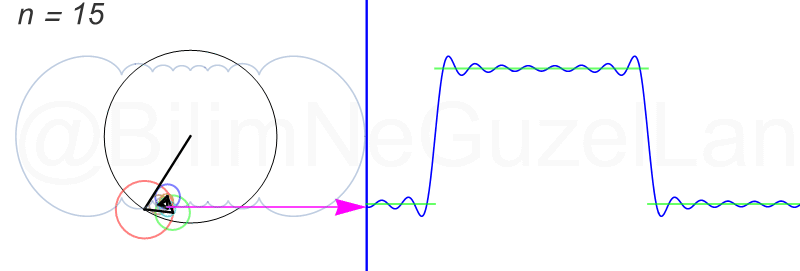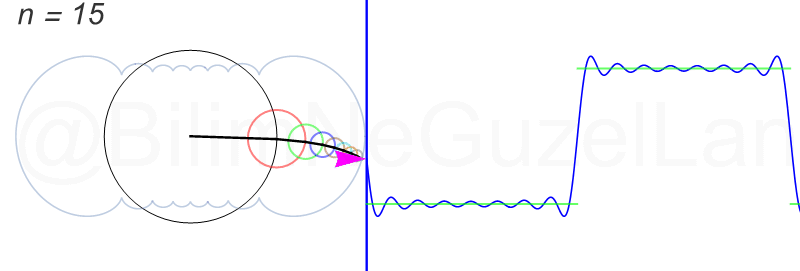
Nasıl, süper değil mi? (｡◕‿◕｡) Sinüs eğrisi bir çember etrafında dönen bir topun gölgesinin aldığı yol olarak düşünülebilir. Bu “kare sinyal” eğrisinde daha fazla terim eklemek, daha küçük yarıçaplı çemberleri, önceki çember etrafında daha hızlı döndürmek demek. Bu dönen çemberlerin frekansları da tek sayı olarak artıyor (hesabı size bırakıyorum). Daha fazla çember ekledikçe (daha fazla n ekledikçe) başlangıçtaki fonksiyonumuza (yeşil eğri) daha fazla yaklaşacağız. Ayrıca, arkaya transparan olarak eklediğim eğrileri fark etmişsinizdir. Bu eğriler de cycloid eğrileri! (başka bir yazımda cycloid eğrilerini anlatmıştım).

Daha fazla terim ekleyerek fonksiyonun kendisine yaklaşmayı şöyle gösterebilirim: \(n = 240\)’a kadar olan terimleri eklersek nasıl görünür?

Devam, şimdi de şöyle “testere ucu” şeklinde bir sinyal alalım ve onu Fourier serisine açalım.

“Testere ucu” sinyali.

Bu fonksiyonu Fourier serisine açtığımızda şu sonuca ulaşıyoruz:

\(f(x) = \displaystyle{\frac{1}{2}} -\displaystyle{  \sum \limits_{n = 1}^{\infty}\left( \frac{1}{n \pi}\right)\sin\left(\frac{n \pi x}{L}\right)}\)

Tekrar, ne kadar terim eklersek bu fonksiyona o kadar daha iyi yaklaşıyoruz. Aşağıdaki animasyonlarda \(n = 1\)’den \(n = 2,3,4,5,6,7,8\)’e kadar olan terimleri ekledim.

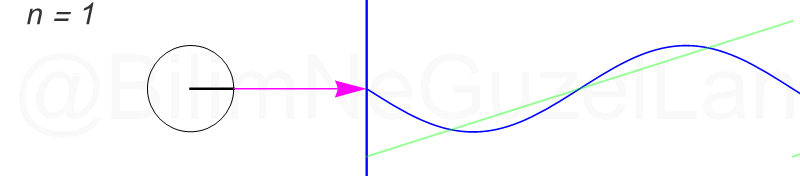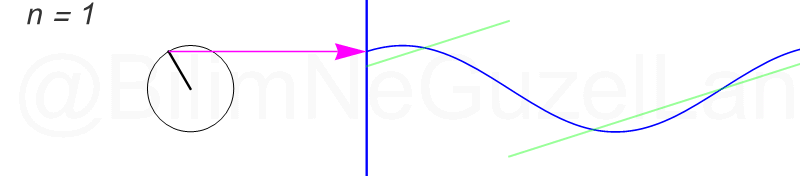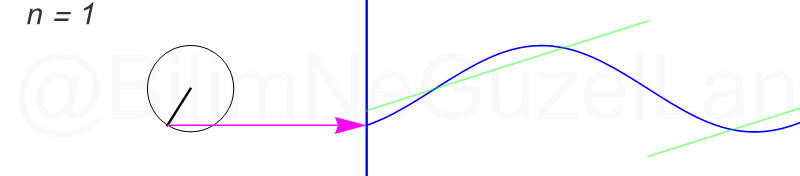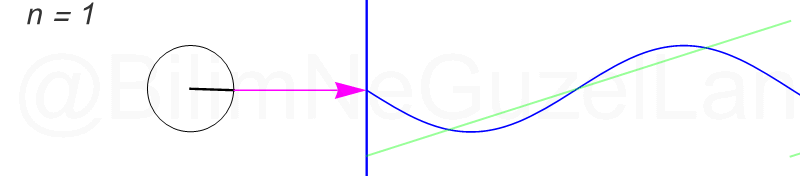
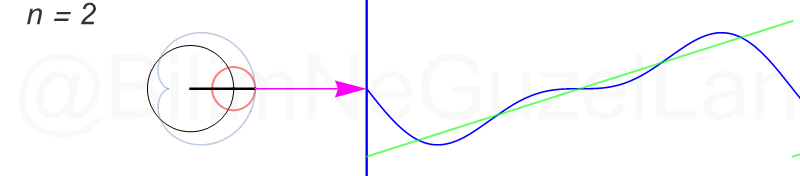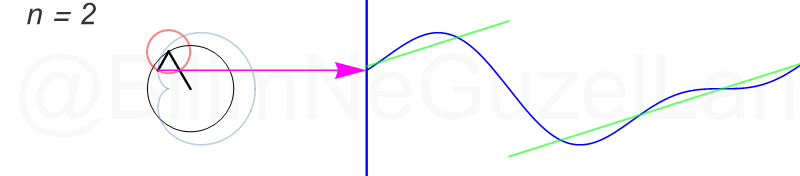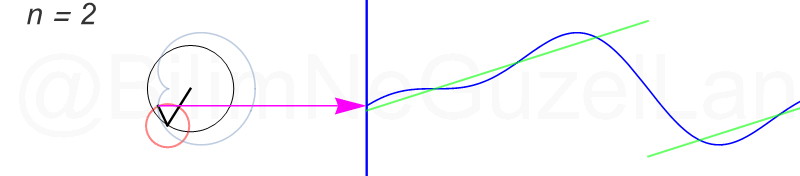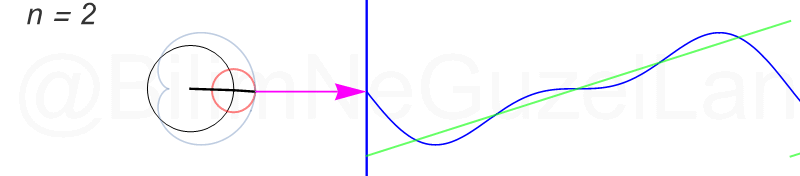
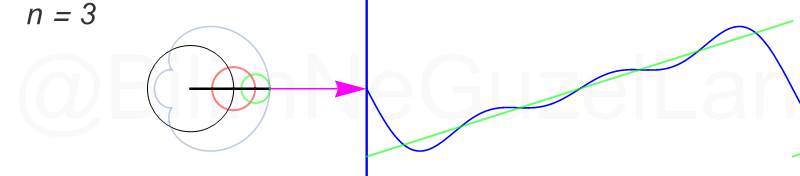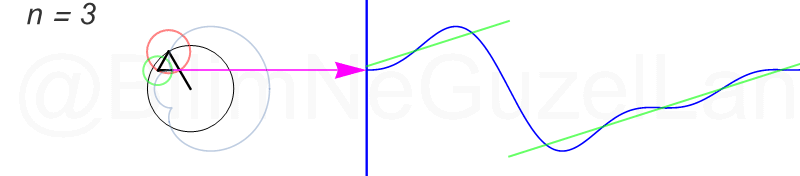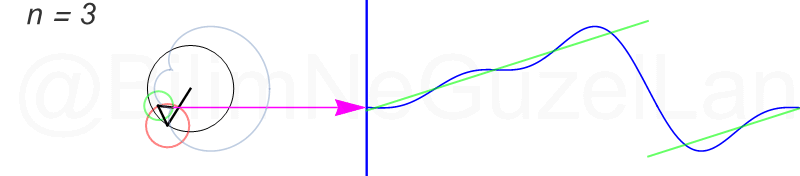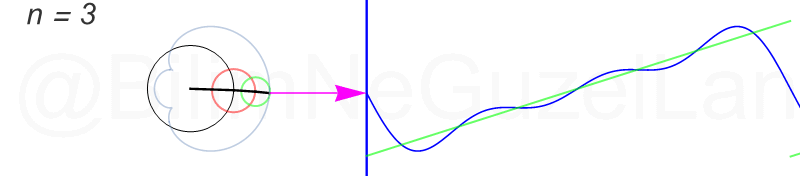
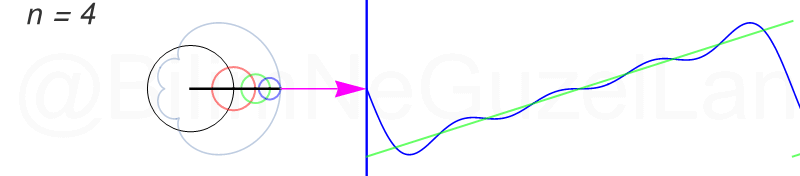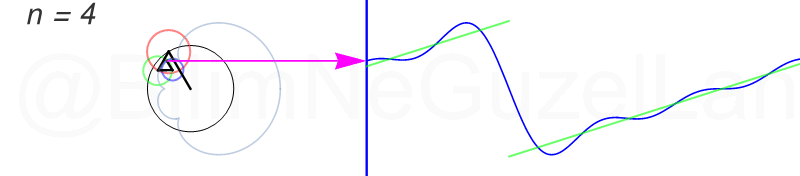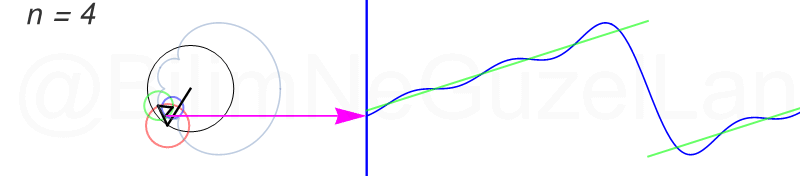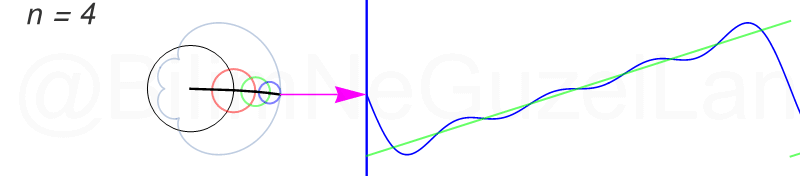
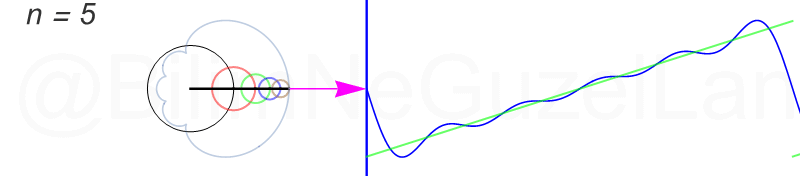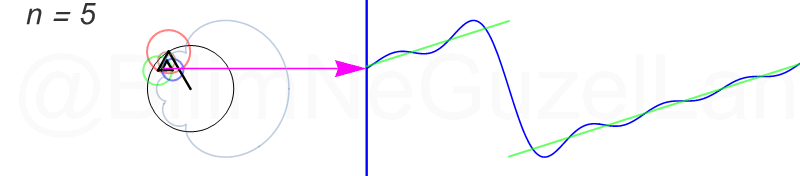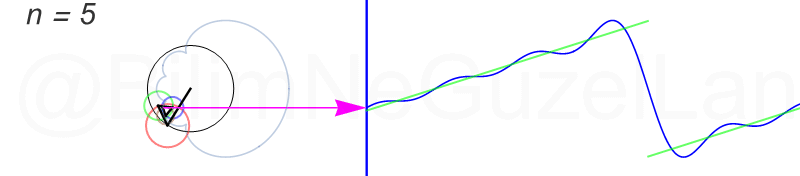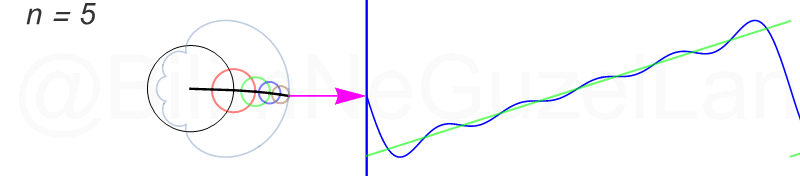
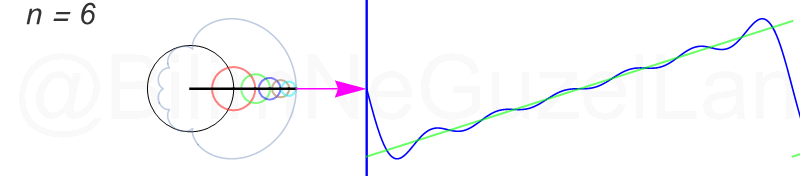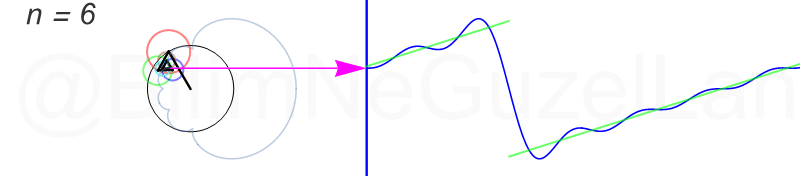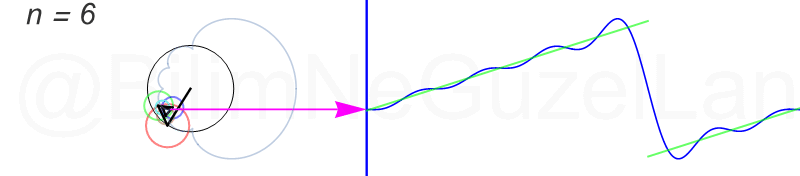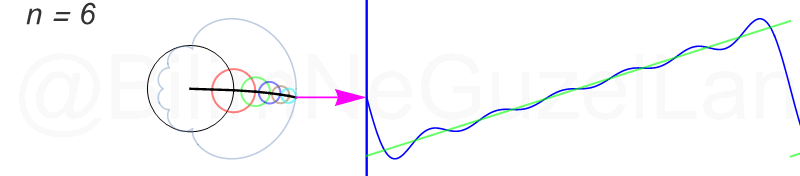
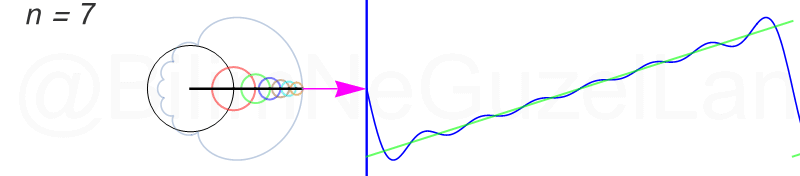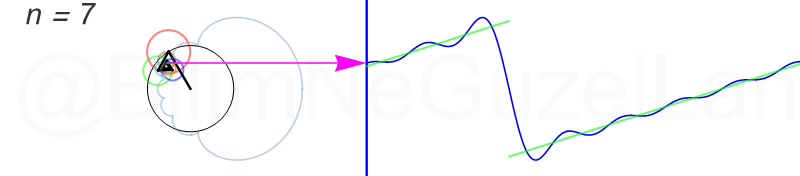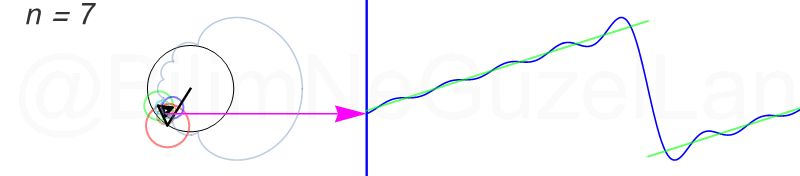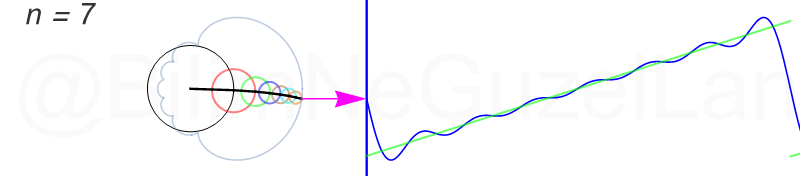
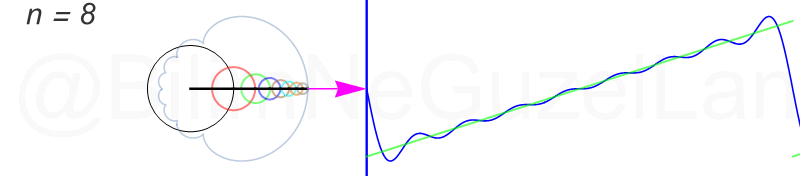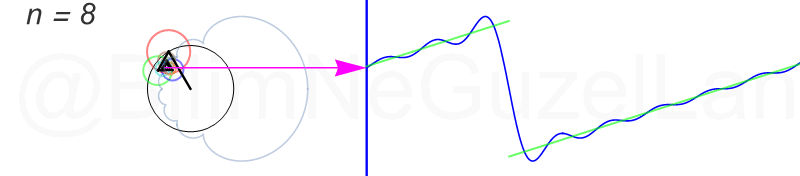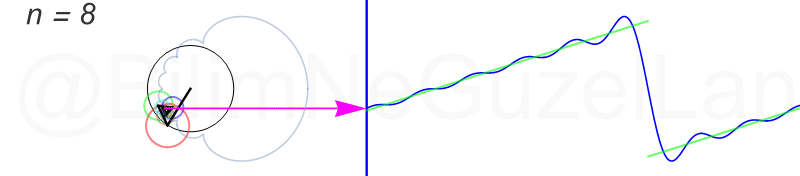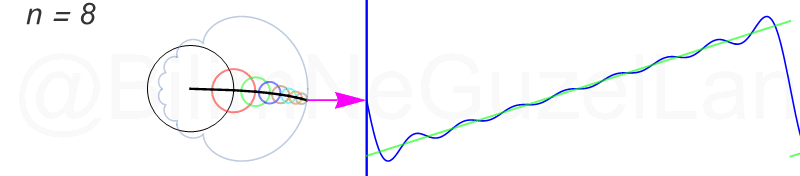Transparan eğri tekrar bir cycloid eğrisi!

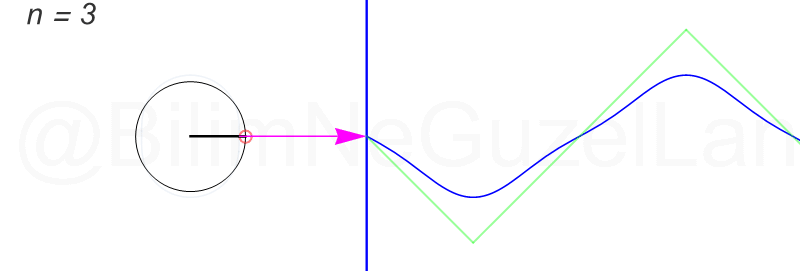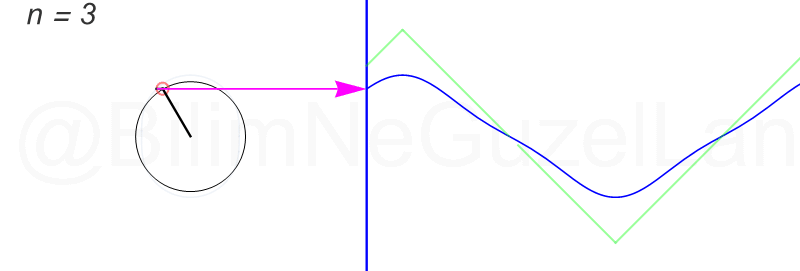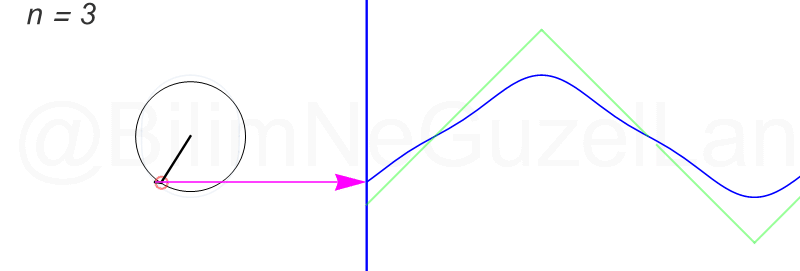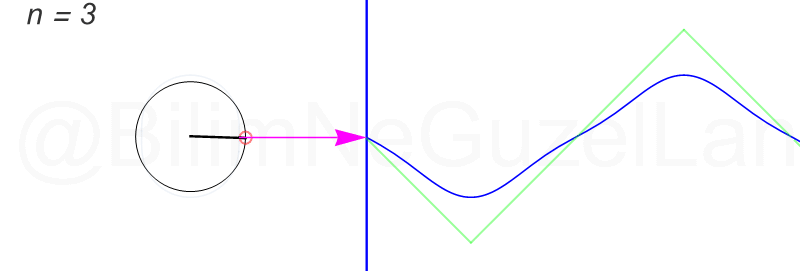
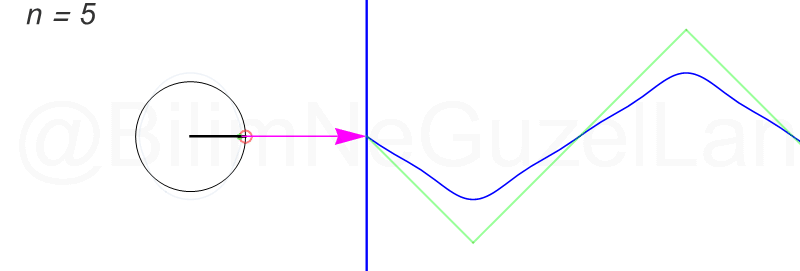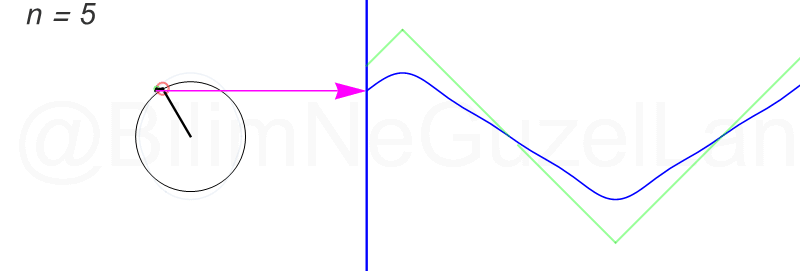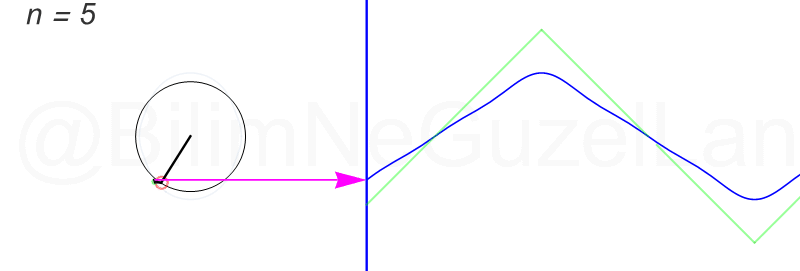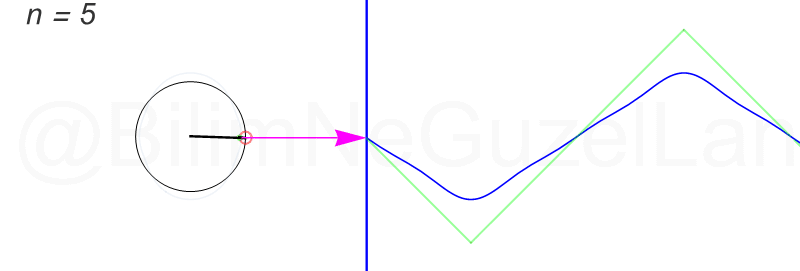
Son olarak, üçgen şekilli bir dalgayı Fourier serisine açacağım, fakat bu öncekiler kadar eğlenceli değil. Bahsi geçen “üçgen dalga” şu:

Ucgen dalga.

Fourier dönüşümünü şöyle buldum:

\(f(x) = \displaystyle{  \sum \limits_{n = 1,3,5,7,…}^{\infty} \left(\frac{8}{\pi^2} \frac{(-1)^{\frac{(n-1)}{2}}}{n^2}\right)\sin\left(\frac{n \pi x}{L}\right)}\)

Daha fazla terim ekledikçe çemberler çok hızlı küçülüyorlar. Öncekiler gibi güzel görünmüyorlar. Olsun, ben ilk üç terimin \(n = 1,3,5\) animasyonlarını ekliyorum:

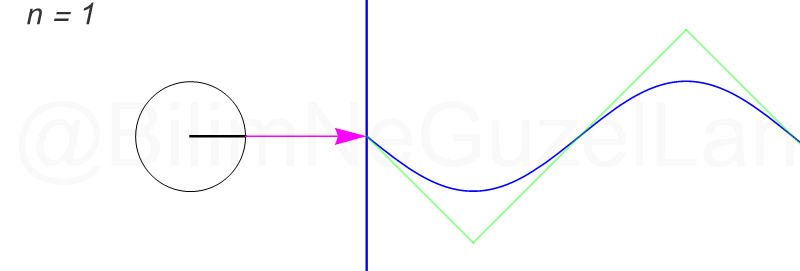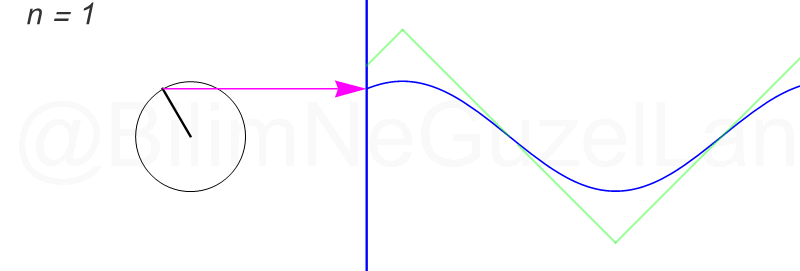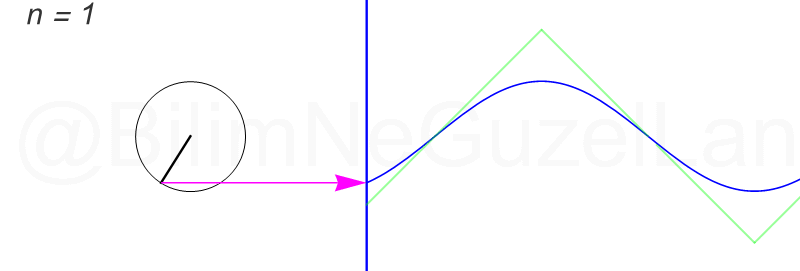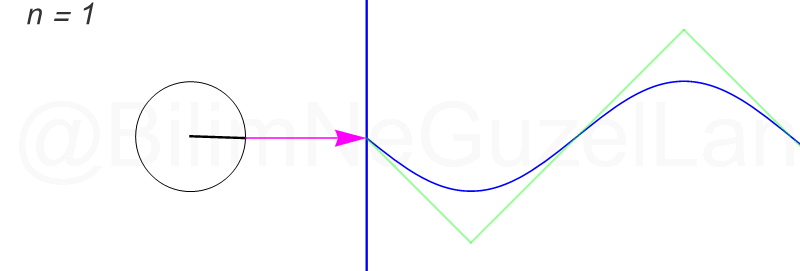
Peki, bu bilgiyi nerede kullanacağız? Çok yerde. Mühendislikte ve temel bilimlerde dört işlem gibi bir şey Fourier analizi. Mesela, elinizde gürültü gibi bir ses dalgası var. Bunu ayrıştırmak istiyorsunuz. Hop, hemen Fuyye amca yetişti yardımınıza. Hangi frekanstan ne kadar dalga olduğunu söyledi.

Gurultu ve Fourier analizi.

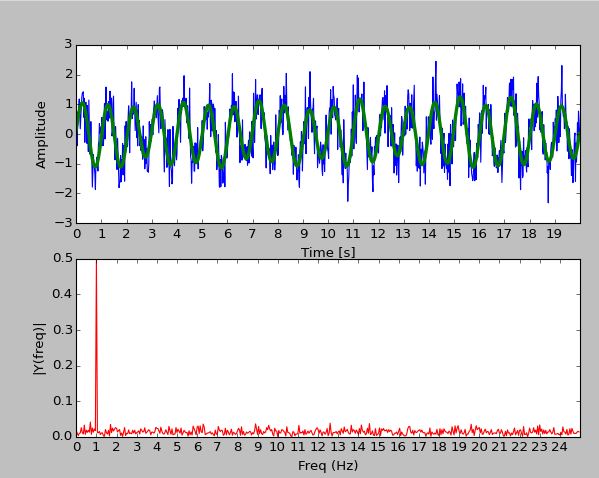
Yukarıdaki görselde, yukarıdaki sesin Fourier dönüşümünü alıyorsunuz ve size bir frekanstan (1 Hz) daha fazla oranda dalga olduğunu söylüyor.

Bunun görüntü işlemede, ses işlemlerinde çok güzel kullanımları var. Burada çok ilginç bir kullanımını göstermek istiyorum.

Bu çalışmada, çok sofistike bir Fourier analizi kullanılarak bir videodan ses çıkarılabiliyor. Yani, komşunuzun salonundaki çiçeği kamera ile sessiz olarak görüntülüyorsunuz, geliyorsunuz ve komşunuzun sizin arkanızdan çevirdiği dedikoduları dinleyebiliyorsunuz.

Yazi ve animasyonlar: Bilgecan Dede

Nicelik değil nitelik daha önemli ama şu kadar kişi okumuş: 104.366
The following two tabs change content below.

Bilgecan Dede

Hukuğa kafası basmadığından meslek okuluna gitti bu. Ondan sonra gâvur bir ustanın yanına çırak verdiler eli iş tutsun diye, çok şükür ustalığını kazanmış ondan, şimdi de usta olmuş çalışıyor. Eli yüzü düzgün biriyle de evermişler. Ben diyorum, “Bak ileride torun combalak olacak, gel bir şirkette işe başla.” Ama dinlemiyor ki, asi biraz bu.

You May Also Like

Mandelbrot & Julia Kümeleri ve Fraktaller

Bilgecan Dede 13

Fourier Serisi yazısına ek:

Bilgecan Dede 8

50 thoughts on “Fuyye Serisi ve Görüntüden Ses Çıkarmak”

Bir cevap yazın

E-posta hesabınız yayımlanmayacak. Gerekli alanlar * ile işaretlenmişlerdir

This site uses Akismet to reduce spam. Learn how your comment data is processed.