Ayıp Olan Bilmemek Değil, Öğrenmemek – Bölüm 1
Bu hafta sonu evde tatlı bir heyecan. Ananız babanız evi toparladılar. Yemekler, tatlılar, börekler falan hazır. Misafir için tüm hazırlıklar tamamlandı. Bilin bakalım, kim geliyor? Yirmi yıldır görüşmediğiniz ikinci dereceden kuzeniniz Cüneyt! Yalnız kendisiyle alakalı ufak bir ayrıntı var. Cüneyt’in anası babası biraz enteresan karakterler olarak kendisini mümkün mertebe popüler kültürden, sosyal aktivitelerden uzak tutmuşlar bu vakte kadar. Kendisinin temel bir matematik eğitimi var ve o da en az sizin kadar zeki bir insan (düşünün artık ne kadar zeki olduğunu) ama çocuğun dünyadan haberi yok. Ne bir televizyon izlemiş ne de oyun oynamış. Enteresan bir karakter anlayacağınız.
Neyse efendim, Cüneytgiller sonunda teşrif ederler. Selam sabah faslı geçildikten sonra, yirmi yıldır görmediğiniz kuzeninizle muhabbeti koyulaştırma vakti gelmiştir. Ne yapalım ne edelim derken gözünüze televizyonun altındaki dolapta duran yılların ahşap tavlası ilişir. Evet, bir el tavla atarak buzları kırabilir ve hafta sonuna iyi bir başlangıç yapabilirsiniz.
– Bir el tavla atalım mı ne dersin?
– Atalım tabii ki ama tavla ne?
– Ya derler ya hani, “şeşi car ve pencü se, severim güzeli gencüse.” Hatta Mirkelam’ın şarkısı var ya, “tavla pulları, zarları” (iç ses: öyle miydi lan?) falan diye gidiyo’?
– Mirkelam mı, o da kim?
(Bu arada, konuyu bölmek istemem ama ne tuhaf bir klipmiş arkadaş bu.)
Anlaşılan o ki daha epey yolunuz var diyalog kurabilmek için. Neyse efendim Cüneyt’le karşılıklı koltuklara geçersiniz, tavla açılır, taşlar dizilir ve zarları elinize alırsınız.

– Büyük atan başlar.
– Büyük derken, neyin büyük olması lazım?
– Zar atıyoruz şimdi ikimiz birden…
– Zar mı, o da ne?
Anlaşıldı, daha da temele inmemiz gerekiyor. Ama tam o esnada aklınıza çakalca bir fikir gelir. Zar nesnesiyle hayatında ilk defa karşılaşmış bir kişiye sorabileceğiniz güzel bir soru vardır.
– Şimdi bu bir zar. Üstünde sayılar var. Bunları fırlatıyoruz ve üstte kalan sayıyı oynuyoruz. Peki, sana bir soru sormak istiyorum. Bu zarı attığımızda 4 gelme ihtimali nedir?
– Ne bileyim abi. Ya gelir ya gelmez?
– Yani?
– 1/2. Ya gelir ya gelmez.
Evet, bu noktada Cüneyt’e “N’aptın abi, zarın 4 gelme ihtimali nasıl 1/2 olur?” diyecek halimiz yok. Çocuğun gerçekten dünyadan haberi yok. Bilmemek ayıp değil, nitekim. Ayıp olan öğrenmemek. Önemli olan Cüneyt’in öğrenmeye açık olup olmayacağı. Bunu test etmek için güzel bir yöntem gelir aklınıza. Zarın tekini alıp atarsınız. Zar 3 gelir.
– Peki şimdi ne diyorsun zarın 4 gelme olasılığına? Görüyorsun zarı attık ve 3 geldi.
– O zaman sıfır. Çünkü hiç gelmedi.
Gidişat fena değil. Cüneyt gözlemlediği olaydan bilgi elde edip “Zarın 4 gelme olayının” ihtimalini kafasında tekrar hesapladı. Zarı bir kez daha atarsınız. Bu sefer 1 gelir.
– Peki şimdi ne düşünüyorsun?
– Hala sıfır. İki defa attık. İkisinde de 4 gelmedi.
Zarı bir kez daha atarsınız. Bu sefer nihayet 4 gelir.
– Peki şimdi zarın 4 gelme ihtimali kaç oldu?
– Üç kere zar attık, sadece birinde 4 geldi. O zaman 1/3 olmalı.
Cüneyt aslında hiç fena gitmiyor. Gayet öğrenmeye açık, her yeni bilgiden sonra olasılık hesabını tekrar yapıyor ve değerini değiştiriyor.
Eğer iyi bir kuzen olursanız, bu deneye sonsuza kadar devam edebilirsiniz. Kullandığınız zar adilse ortalama her altı atıştan birinde 4 geleceği için, Cüneyt en sonunda zarın 4 gelme olasılığının 1/6 olacağını hesaplayacaktır.
Peki bizim Cüneyt’ten farkımız neydi? Neden biz, bir zarın 4 gelme olasılığının 1/6 olduğunu biliyoruz da Cüneyt bilmiyor? Çünkü biz küçüklüğümüzden beri zar atarak oyun oynadık. Bir zarın ortalama altı defada bir kere 4 geldiğini tecrübeyle öğrendik. Üstüne üstlük okulda geometri dersi aldık ve küp şeklindeki zarların altı eşit yüzeyi olduğunu öğrendik. Yani Cüneyt’ten farklı olarak hem tecrübemiz hem de eğitimimiz var. Peki, şöyle bir soru sorsam cevabınız ne olur?
– Durağa otuz dakikada bir gelen otobüsü, kaç dakika sonra geleceğini bilmeden beklemeye başladınız. Bu otobüsün ilk on dakika içinde gelme olasılığı nedir?
Peki, bu?
– Elinizde bir deste iskambil kâğıdı var. En üstteki kâğıdın kupa olma ihtimali nedir?
Peki, ya bu?
– Ortalama iki yılda patlayan bir ampulün, ilk yıl içinde patlama olasılığı nedir? (Burada kastedilen ampul, o ampul değil.)
Birinci soru için bir fikir yürütebiliyoruz sanki. Hani insanın 10/30 = 1/3 diyesi geliyor, değil mi? İkinci soru da kolay gibi. Kâğıtlarda dört farklı simge olduğu için, olasılık dörtte bir diyebiliriz. Peki ya üçüncü soru? Herkesin üç aşağı beş yukarı fikri vardır tabii ama bu durumda pek çoğumuz bu soru için birer Cüneyt’e dönüşüyoruz. Çünkü ampulun patlama süresi konusunda hiçbir bilgi birikimine sahip değiliz. Yani birer Cüneyt’iz.
Burada bir dakika duralım. “Olasılık nedir?” diye sorsam ne dersiniz? Kendime soruyorum da, “bir şeyin olma ihtimali” yok lan, ihtimal zaten olasılıkla aynı şey. Valla o kadar okulunu okudum ama Tabu’da çıksa zor anlatırım. Şöyle desek daha mı iyi olur?
Kesin bilgi sahibi olmadığımız bir olayın olabilirliğini 0’dan 1’e kadar puanladığımız bir sistem. Puan 1’se kesinlikle olacak, 0’sa kesinlikle olmayacak. Puan 1’e yaklaştıkça, olay daha bir olabilir.
Düşünüyorum da gayet başarılı bir puanlama sistemi olmuş. Bugün tavla oynayan dedenize, Güney Amerikalı bir çiftçiye, Kamboçyalı bir esnafa herhangi bir şeyin ihtimalini sorsanız kendisi size 0’la 1 arasında bir sayı verecektir. Bu kadar soyut bir kavramın böylesi evrensel bir kullanışının olması gerçekten enteresan.
Burada kilit nokta, olayın olup olmadığı veya olmayacağı konusunda kesin bir bilgimizin olmaması. O yüzden olasılıklar kullanarak süreci daha iyi anlamaya çalışıyoruz. Yani zarın 4 gelip gelmeyeceğini bilmiyoruz. Eğer zarın atılmasını beklersek kendisinin 4 gelip gelmeyeceğini öğrenebiliriz. Başka bir yöntem de zarın atılış yönünü, elimizdeki duruş şeklini, yer çekimini, havanın uygulayacağı sürtünmeyi, tavlanın şeklini, pulların yerini ve daha pek çok faktörü kullanarak bir hesap yapıp belli bir hata payıyla zarın kaç geleceğini hesaplamak. Fakat bu, tavla gibi basit bir oyun için fazla detaylı ve yorucu bir bilimsel çalışma olur. O yüzden kolaya kaçıp olasılık 1/6’dır demeyi tercih ediyoruz. Benzer şekilde, destenin üstündeki kağıdın ne olduğu da aslında belirli, fakat biz bu bilgiye sahip değiliz. O yüzden kupa olma ihtimaline 1/4 demekle yetiniyoruz.

Bilim dünyasında olasılık konusunun ele alınışı ise şöyle oluyor: Değerini bilmediğimiz ve bir olasılık hesaplayıp tahmin etmek istediğimiz olguya “rassal değişken” (random variable) adını veriyoruz. Yani zarın üstte kalan yüzü, bir rassal değişken. Onun değeri 1 veya 2 değil. Ama 1 veya 2 olabilir. Hatta 1’den 6’ya kadar değişebilir. Destenin en üstünde kalan kâğıt da başka bir rassal değişken ve kupa, maça, sinek, karo değerlerini alabilir. Ampulün yaşam süresi de başka bir rassal değişken. Rassal değişkenleri belirledikten sonra kendisinin çeşitli değerlerinin olasılığını hesaplamaya geliyor sıra. Bu tabii ki zar ve destenin üstündeki kâğıt gibi rassal değişkenler için gayet kolay. Ama sen gel bakalım, kolaysa ortalama ömrü iki sene olan ampulün bir sene içinde patlama ihtimalini hesapla. Evet, pek kolay değil. Bunun için şirketlerin kalite kontrol departmanları pek çok deney ve test yapıyor ve ellerine çıka çıka kocaman bir grafik çıkıyor. Rassal değişkenin her değeri için farklı bir olasılık. Biz buna “olasılık dağılım fonksiyonu” (probability distribution function) adını veriyoruz. Bu grafiği elde ettikten sonrası ise kolay. Hemen hemen her istediğimiz şeyin olasılığını hesaplayabiliyoruz. Mesela ampulün patlama süresinin eksponansiyel bir dağılım fonksiyonu olduğu tahmin edilmiş bu vakte kadar [1]. Bu varsayımla kendisinin olasılık dağılım fonksiyonu işte şöyle bir şey. Burada lambda, birim zamanda ortalama patlama sayısı.
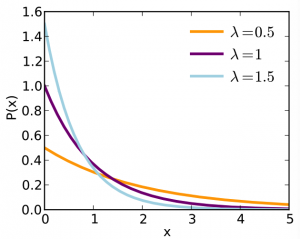
Eğer bir yıldan önce patlama ihtimalini bulmak istiyorsak, grafiğin x’in 1’den küçük olduğu kısmın alanını hesap etmemiz gerekiyor. Peki hangi lambda’lı grafiği kullanacağız? Onu da şöyle bulabiliriz. Ampulun ortalama iki yılda patlaması, bir yılda ortalama 1/2 patlama demek. O yüzden lambda = 1/2 olan grafiğe bakacağız. O alanı hesap edecek olan formül de elimizde, buyrunuz. Sadece t yerine 1 koymamız gerekiyor ve cevap 0.39346 çıkıyor.
\(1 – e^{-\lambda t} \)
Bu kadar kafa yorduktan sonra olasılık için yeni bir tanım buldum sevgili dostlar. Olasılık geleceği anlamak ve sayısal olarak değerlendirmek için tek şansımız. Yarın %60 ihtimalle yağmur yağabilir, o zaman şemsiyemi hazır edeyim. Beşiktaş %70 ihtimalle bu maçı alır, o zaman iddaa’da parayı basayım. İyi bir okula kapağı atarsam %90 hayatımı kurtarırım, o zaman gidip çalışayım. Biraz daha bilimsel örnekler bulalım:
– Bir market sahibi olarak organik limonun bu hafta x kg satılacağı ihtimalini hesaplarsam limonu getirttiğim yerden ne zaman ve ne kadar sipariş etmem gerektiğini de hesaplayabilirim. Böylece ne dükkanımda fazla limon tutarım ve limonlar çürür ne de limonsuz kalıp potansiyel satışları kaçırırım. -> Yöneylem araştırması/optimizasyon.
– Bir elektronunun t+1 zamanında x noktasında olma ihtimalini hesaplamak istiyorum. Neden? Çünkü kauntum fiziği bunu gerektiriyor. O zaman alır Schrödinger’in kuantum alan denklemini kullanıp hesabımı yaparım. -> Kuantum fiziği
Peki ya rassal değişkenler? Koskaca oyun endüstrisi, rassal değişken üreticileri (random number generator) üstüne kurulu dostlar. Kullandığımız bu üreticiler oyunlara şans faktörü katmakla kalmayıp her oynanan oyunun farklı olmasını da sağlıyorlar. Rassal değişken üreticilerinin en basiti “zar.” İnsanlığın oyun oynayabilmek için icat ettiği, gayet orijinal bir ürün. Oynadığımız bilgisayar oyunlarının çoğunda da birer rassal değişken üreticisi mevcut. Elbette, oyunlarda kullanılanlar birer küçük yazılım halinde.
Konuyu biraz dağıttık sanki. Cüneyt’i evde tavlanın başında bıraktık, lak lak yapıyoruz. İşimize geri dönelim. Ne diyorduk? Ayıp olan bilmemek değil, öğrenmemek. Madem öyle, gariban misafirimiz Cüneyt’i biraz daha zorlayalım mı, ne dersiniz? Bu arada Cüneyt kardeşimiz deneye yanıla zarın 4 gelme ihtimalinin 6’da 1 olduğunu biz gevezelik yaparken öğrenmiş.
Cüneyt’e gözlerini kapamasını söylediniz ve zarı tekrar attınız.
– Peki, Cüneyt. Sana yine zarın 4 gelme ihtimalini soracağım ama bir de ek bilgi veriyorum. Zar 5’ten daha küçük geldi. Şimdi zarın 4 gelme ihtimali nedir?
Devamı burada.
Not: Görselleri Wikipedia, Murat Menteş’in twitter’i ve Mirkelam’ın kliplerinden apardık.
[1] https://punkrockor.com/2011/02/10/is-anything-really-exponentially-distributed/
Hafız Lakyab
Yazar: Hafız Lakyab (tümünü gör)
- Dev Kütleli Bir Kara Deliğin Olması Gereken Yer, Galaksisinin Merkezi midir? - 17 Eylül 2019
- Bana kod yazmayı öğret baba – Bölüm 9 - 10 Mart 2019
- Bana kod yazmayı öğret baba – Bölüm 8 - 24 Şubat 2019
- Bana kod yazmayı öğret baba – Bölüm 7 - 10 Şubat 2019
- Bana kod yazmayı öğret baba – Bölüm 6 - 27 Ocak 2019




