Fourier Serisi yazısına ek:

Öncelikle Destin Sandlin’e ve herkese destekleri ve ilgileri için teşekkür ederim. Bu yazıda videoda bana sorulmuş bir kaç soruya cevap vereceğim. Herhalde bundan sonra da Fourier serisi hakkında yazmam, çünkü yeteri kadar yazdım ve kendimi tekrar etmekten hoşlanmıyorum 🙂 Bir popüler bilim sitesine göre biraz teknik bir yazı oldu, o yüzden şimdiden özür dilerim.

S1: Bir poligonu (kare, beşgen, altigen vs.) Fourier serisine açmak mümkün müdür?

Daniel Shiffman’a teşekkür ederim. Evet, bir poligon periyodik bir eğri olarak düşünülebileceğinden, Fourier serisine açılabilir. Burada nasıl açılabileceğini göstermek istiyorum:

Diyelim ki \(f(x)\) duzgun bir n-gen’i temsil etsin.

Hedefimiz, bu \(f(x)\) fonksiyonunu Fourier serisine açmak:

\(\displaystyle{ f(x) =\frac{1}{2} a_0 + \sum \limits_{n} \left(a_n \cos(n x) + b_n \sin(n x)\right)}\)

Ama, bunun yerine bu Fourier serisini başka bir formda yazayım, çünkü hesaplamaları yapmak daha kolay olacak:

\(\displaystyle{f(x) =\sum \limits_{m = -\infty}^{\infty} c_m e^{i m x}}\),

cunku, \(e^x = \cos x + i \sin x\), ve \(i = \sqrt{-1}\), kompleks sayi. Pekala, Fourier serisinin esprisi bu sabitleri hesaplamak:

\(\displaystyle{c_m = \frac{1}{2 \pi} \int \limits_{0}^{2\pi}f(x) e^{-i m x} dx}\)

İlk iş olarak poligonu n ayrı parçaya ayırabilirim:

\(\displaystyle{c_m = \frac{1}{2 \pi} \sum \limits_{j = 0}^n \int \limits_{x_j}^{x_{j+1}}f(x) e^{-i m x} dx}\),

öyle ki, her bir integral sadece düz bir çizgi üzerinde olsun. Kısmı ıntegrasyonu kullanırım ve bu terimleri biraz değiştirebilirim:

\(\displaystyle{ \int \limits_{x_j}^{x_{j+1}}f(x) e^{-i m x} dx = \left.\left[f(x)\frac{e^{-im x}}{-i m}\right]\right|_{x_{j}}^{x_{j+1}} – \int \limits_{x_j}^{x_{j+1}}s_j \frac{e^{-im x}}{-i m}dx}\).

\(s_j \) \(f(x)\)’in \(j\). parcadaki egimi, \(s_j = df/dt\) ve bu bir sabit! Tüm poligon üzerinden toplam aldıktan sonra ilk terim sıfır olur, çünkü başlangıç noktamız zaten \(f(x)\)’in periyodik olduğu idi! İkinci terime kaldık. Ama bunu çözmek çok kolay:

\(\displaystyle{c_m = \frac{1}{2 \pi} \sum \limits_{j = 0}^n \int \limits_{x_j}^{x_{j+1}}s_j\frac{e^{-im x}}{i m} dx} = -\frac{1}{2\pi m^2} \sum \limits_{j = 0}^n \sigma_j e^{-i m x_j} \),

\(\sigma_j = s_j – s_{j-1}\). Ama, tekrar bu egri periyodik oldugundan, \(s_0 = s_n\). Buradan, \(n\). parcanin egimini su sekilde bulurum:

\(s_{j-1} = \frac{1}{2\pi}\sum \limits_{j = 0}^{n-1}x_j \sigma_j\).

Şimdi, bazı poligonların animasyonlarını, yukarıda yazdığım kurallar çerçevesinde ekleyeceğim. Gerçek sayı kısmı \(x\), sanal kısmı \(y\) olacak. Poligonu merkeze yerleştirmek istiyorum, bu yüzden \(j = 0\) terimini sıfıra eşitledim. Bu yüzden, toplamı biraz değiştirebilirim:

\(\displaystyle{f(x) =\sum \limits_{l = 1 mod 2n} \frac{e^{i (2 + n l) x}}{(2+ nl)^2}}\)

Buraya bir kaç tane poligonu ekliyorum:

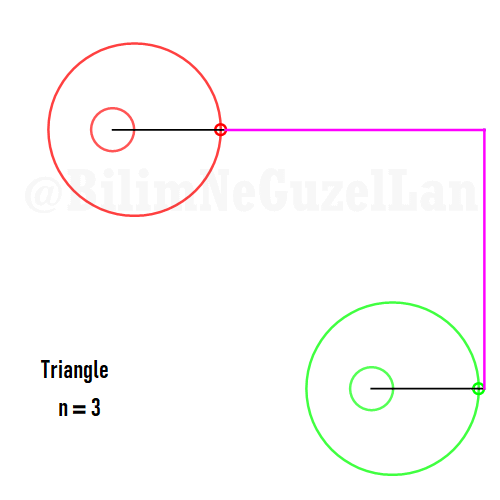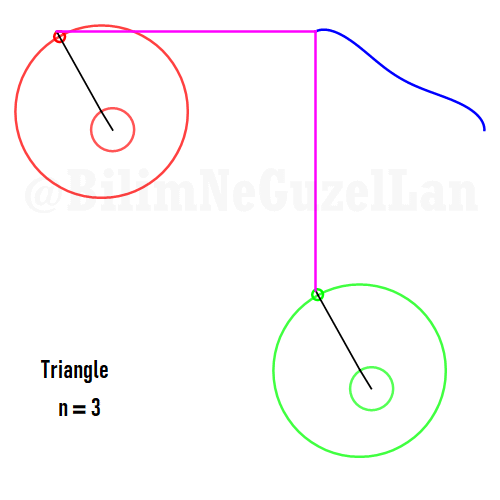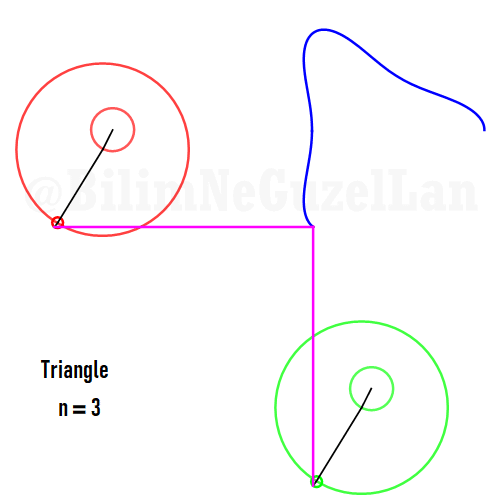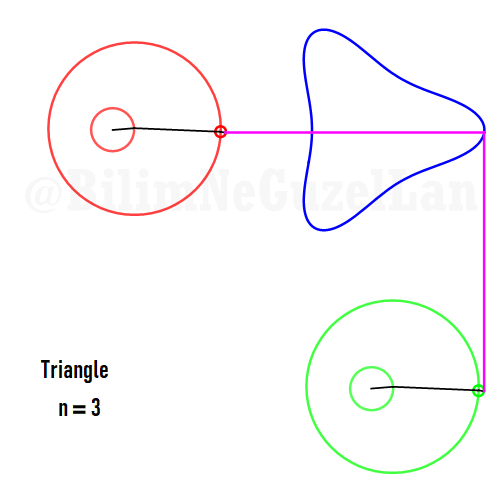
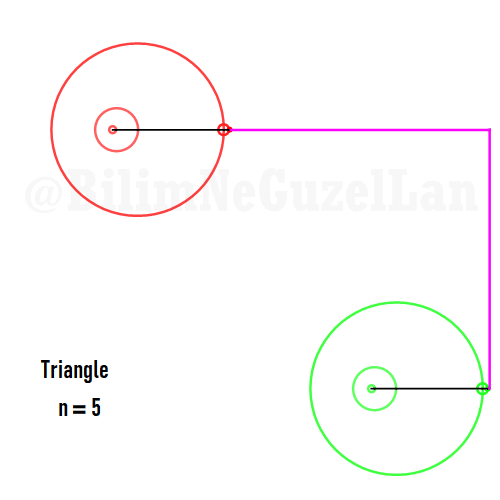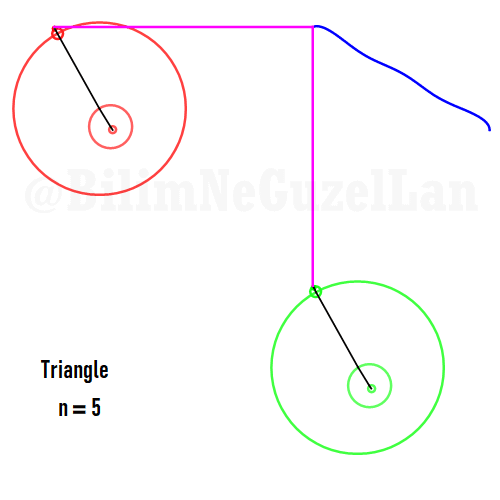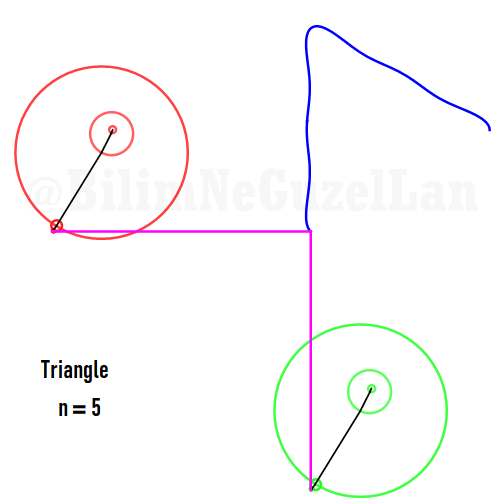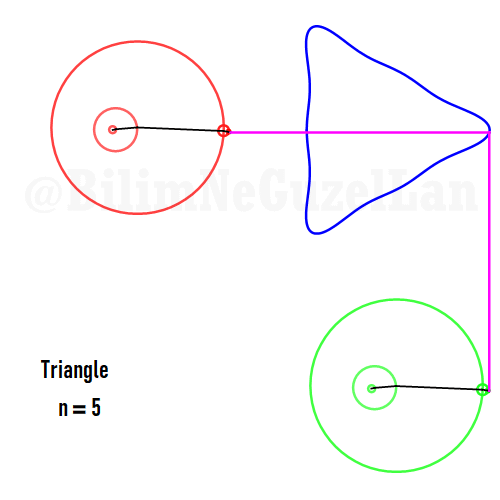
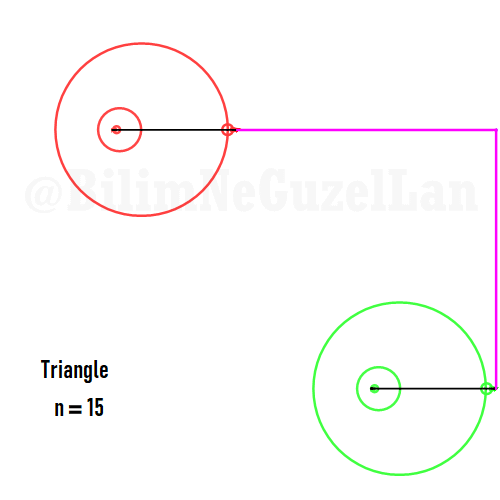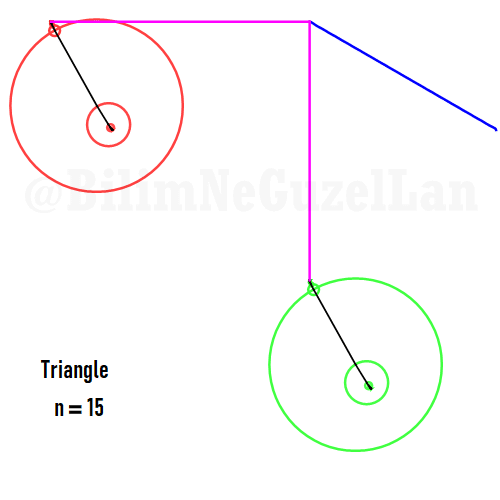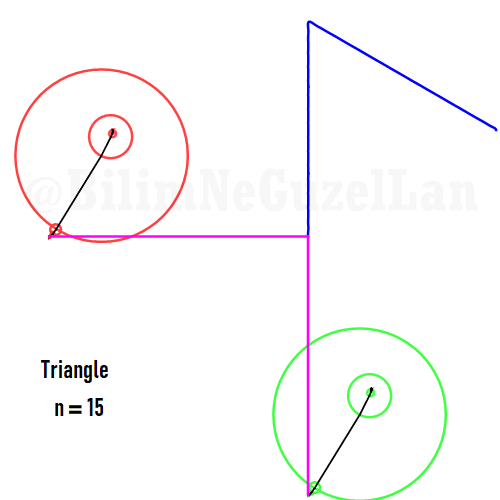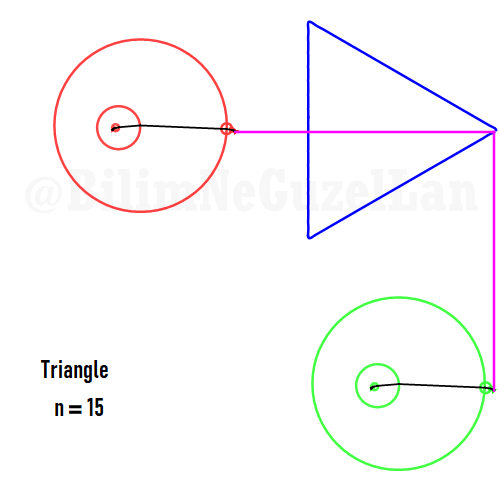
Kare:

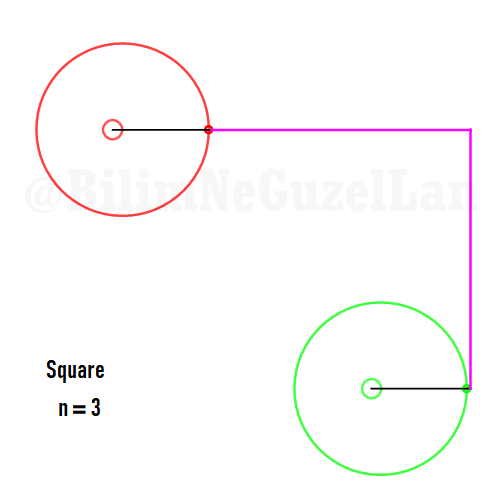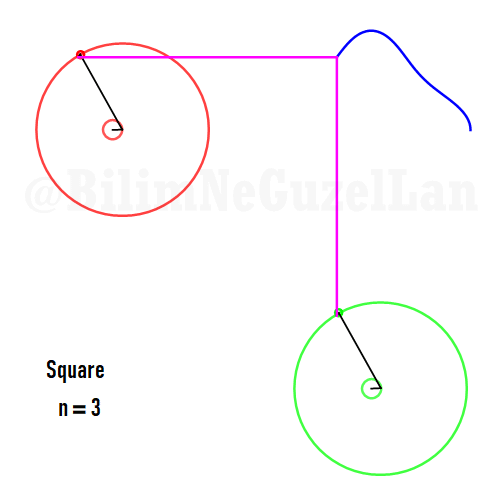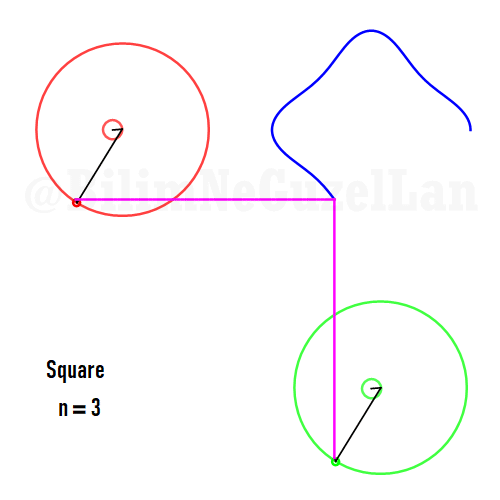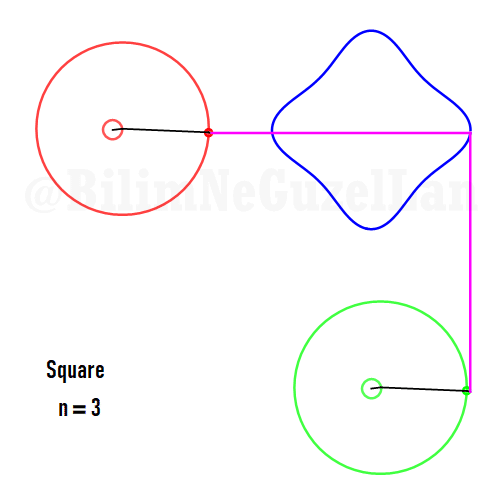
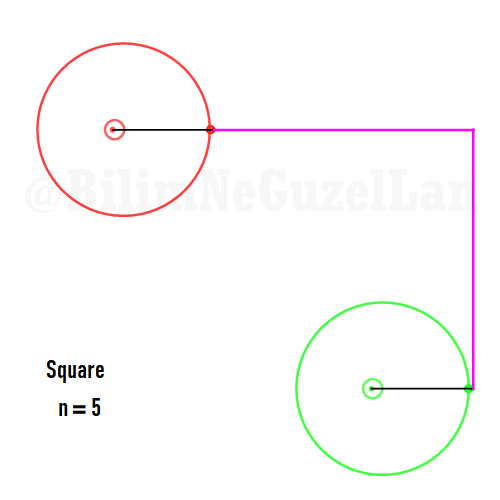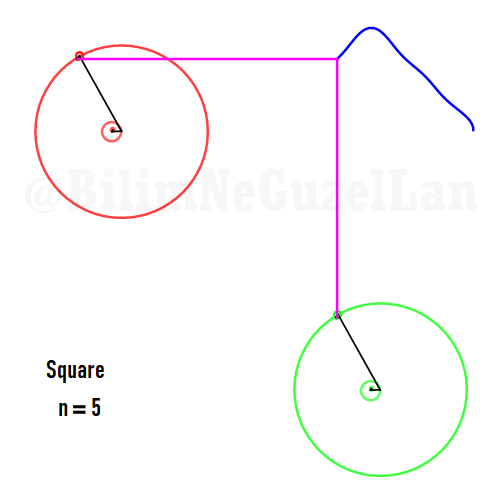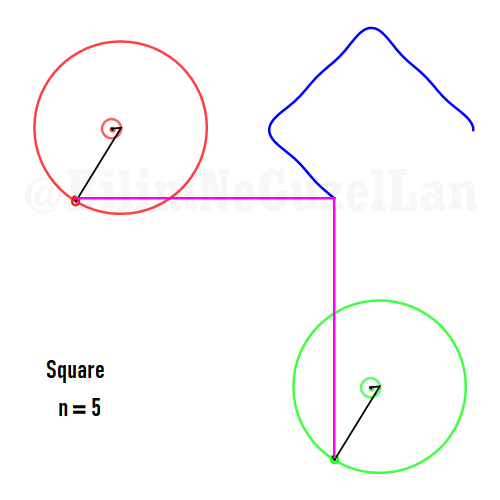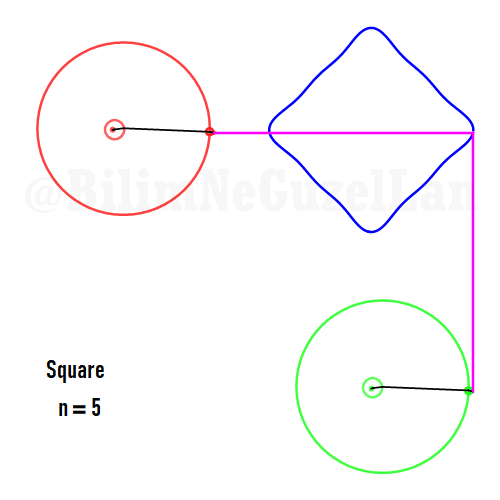
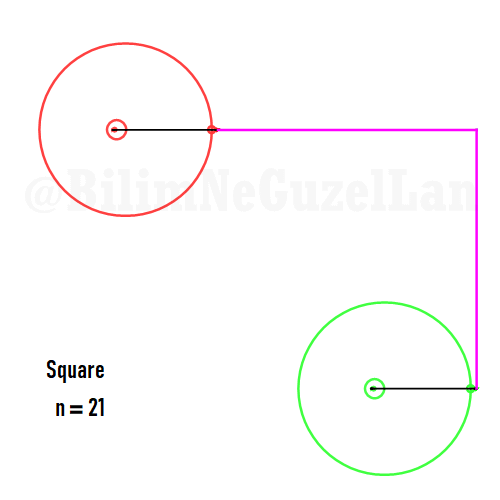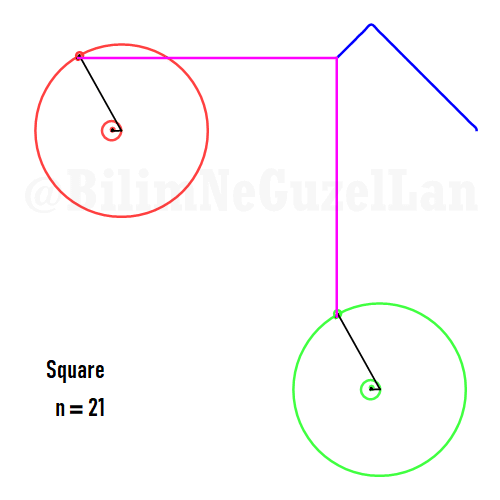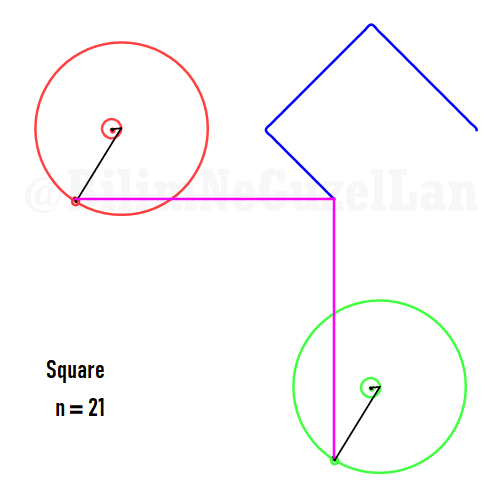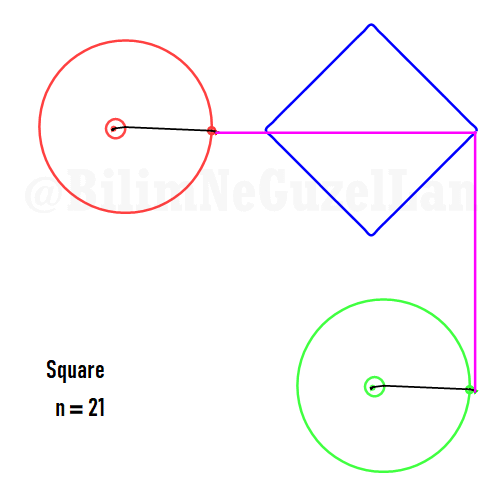
Besgen:

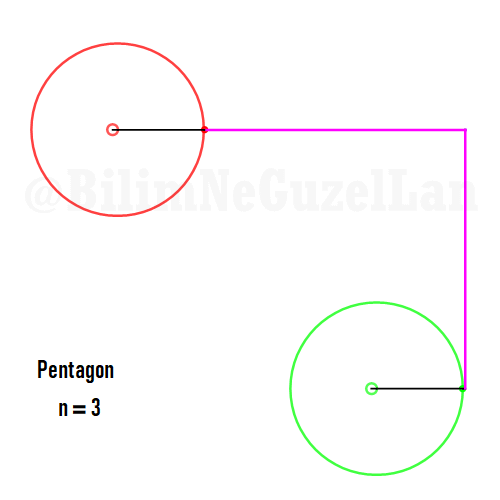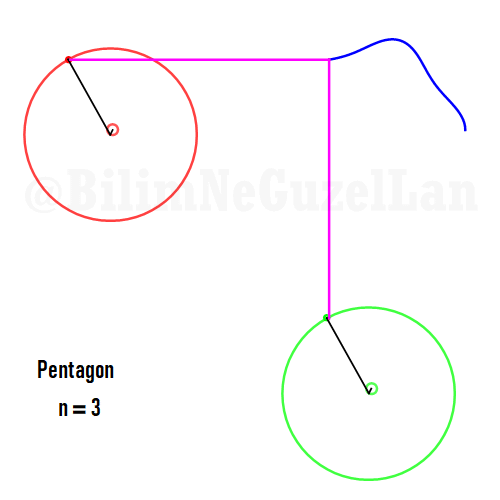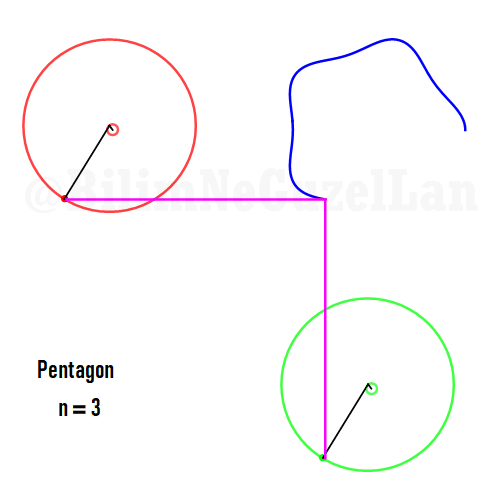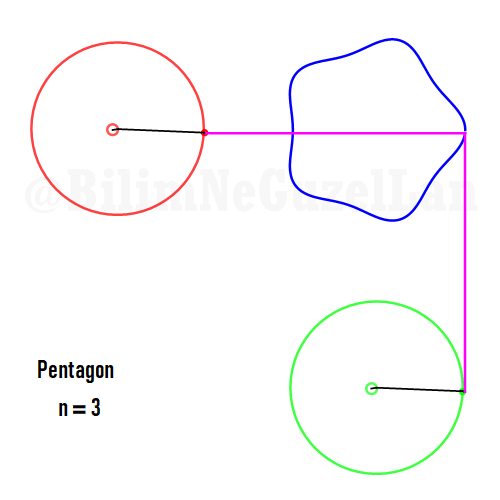
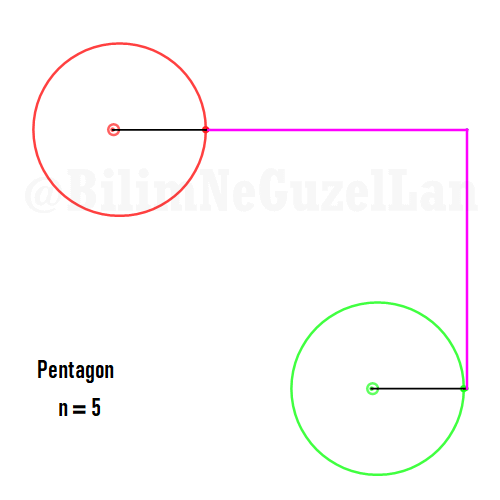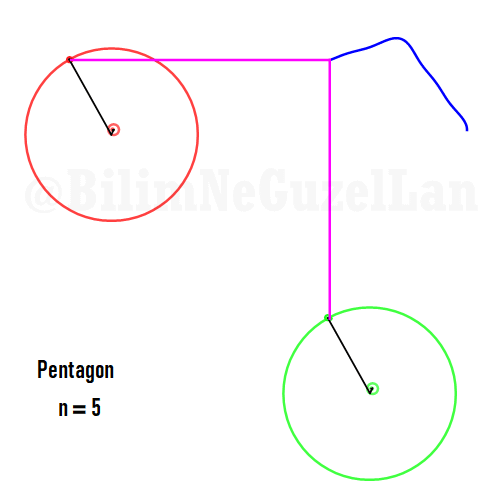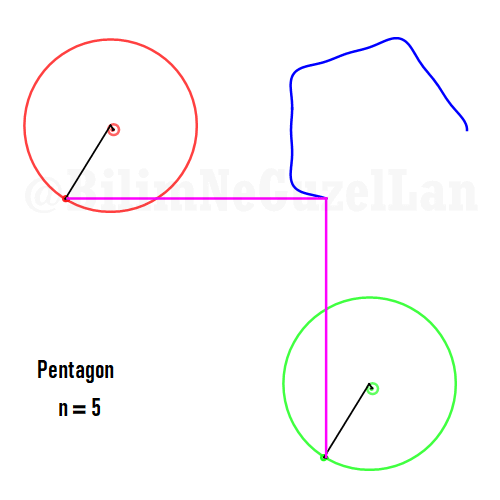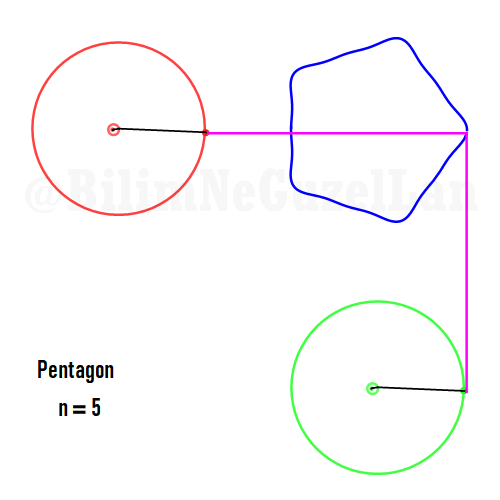
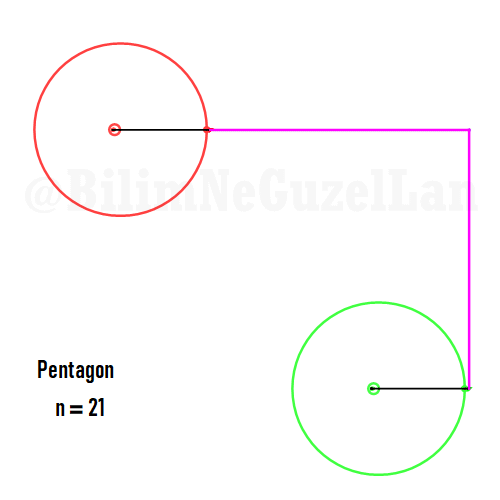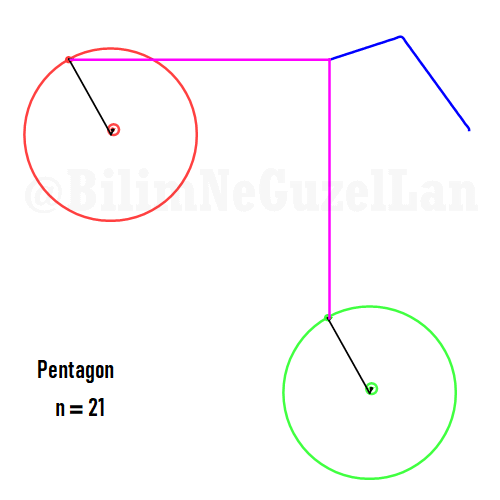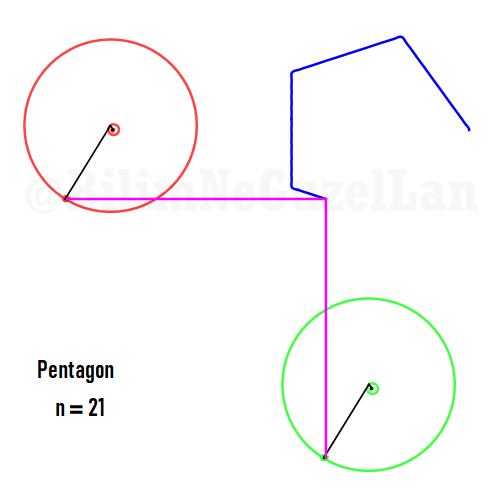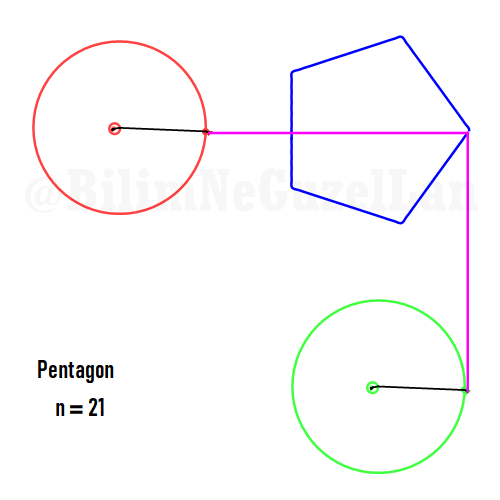
Aynı zamanda, daha güzel şekiller, yıldızlar vs. yapmak da mümkün. Sadece asımetrik harmoniklerle iki tane poligonun süperpozisyonunu alacaksınız (yani bildiğiniz toplayacaksınız). Asımetrik harmonik derken, \(n_1\) ve \(n_2\) arasında ortak bölen olmamasını kast ediyorum.

\(\displaystyle{f(x) =\sum \limits_{l = 1 mod 2n} \frac{e^{i (n_1 + n_2 l) x}}{(n_1+ n_2 l)^2}}\)

Buraya bir yıldız şeklini koyuyorum:

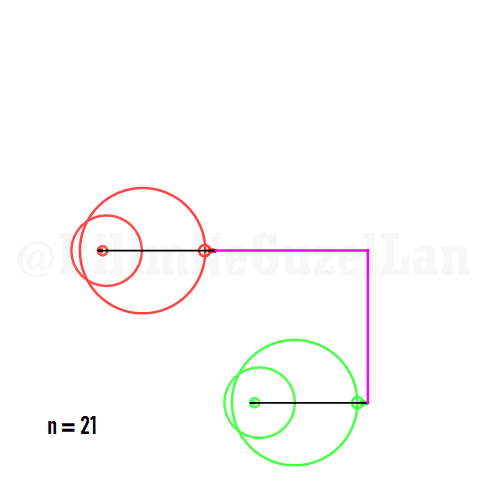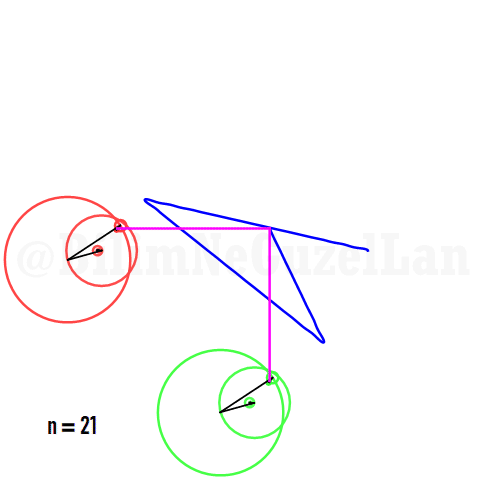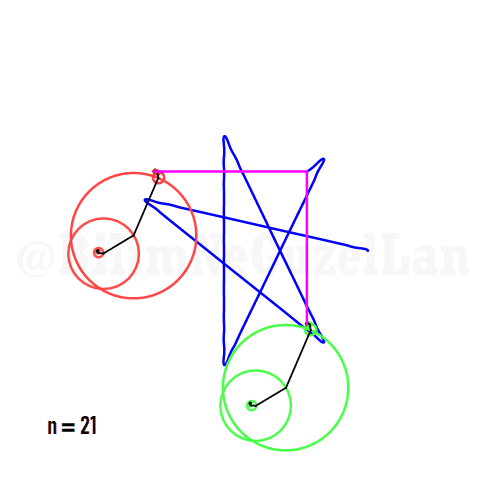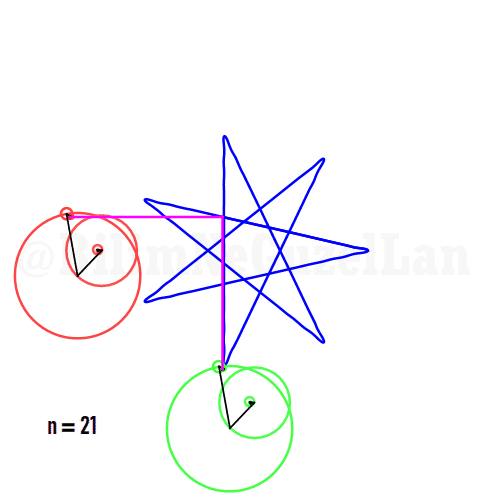
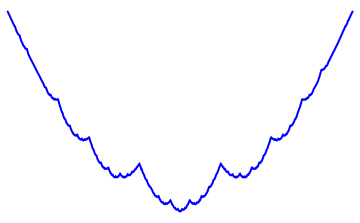
Q2: Eğer harmonikler Fibonaccı dizisini, 1, 1, 2, 3, 5, 8, 13, 21, vs., izlerse eğri nasıl görünür?

Laura Kinnischtzke’ye önerisi için teşekkür ederim. Polar olarak şu şekilde yazabilirim,

\(\displaystyle{ f(\theta) = \sum \limits_{n \in F_n} \left(\frac{c}{n} \cos(n \theta)  + \frac{c}{n} \sin(n \theta) \right)}\)

\(F_n = F_{n-1} + F_{n-2}\), Fibonacci dizisi.

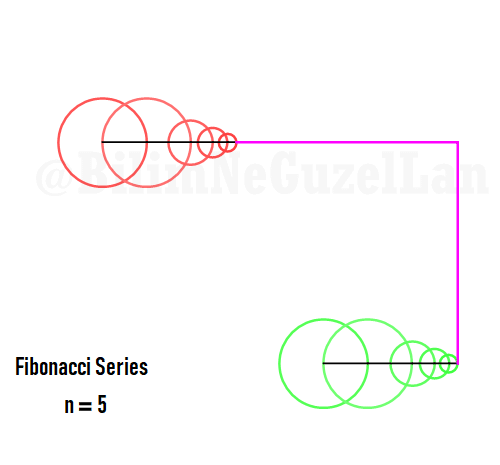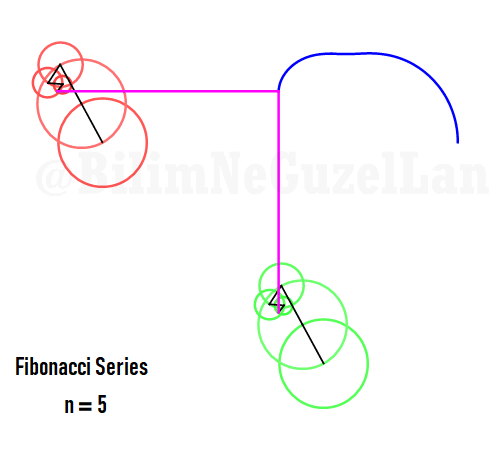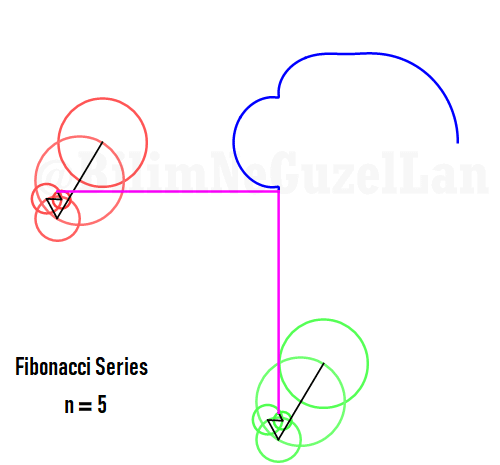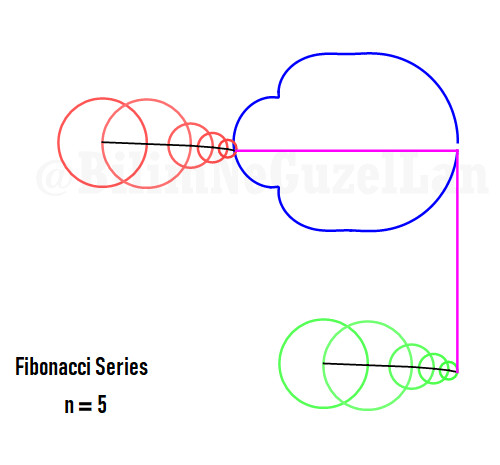
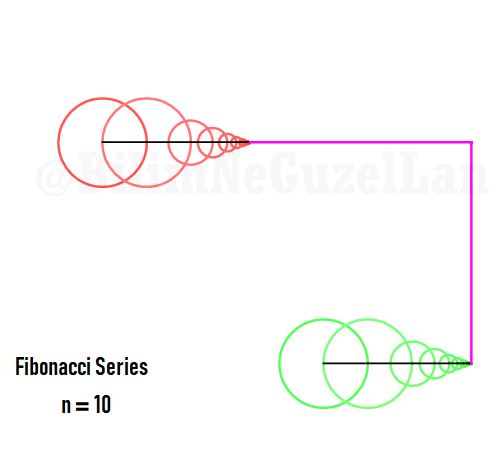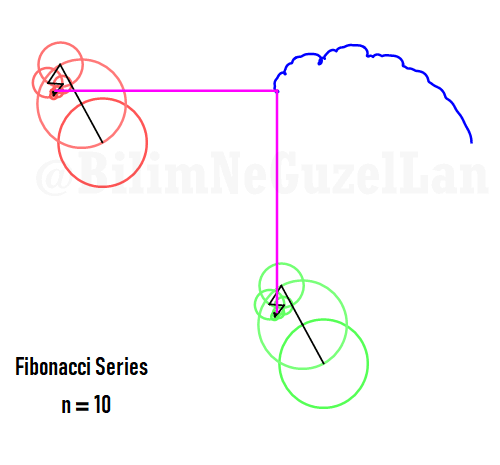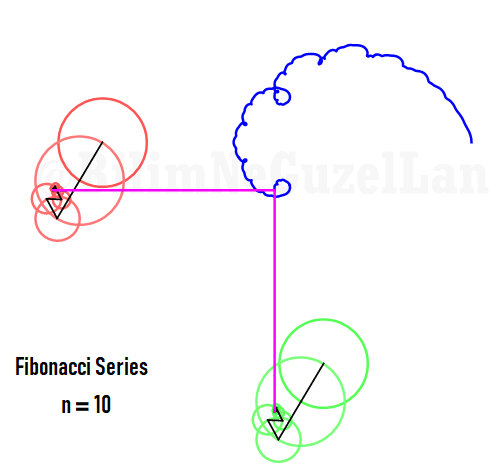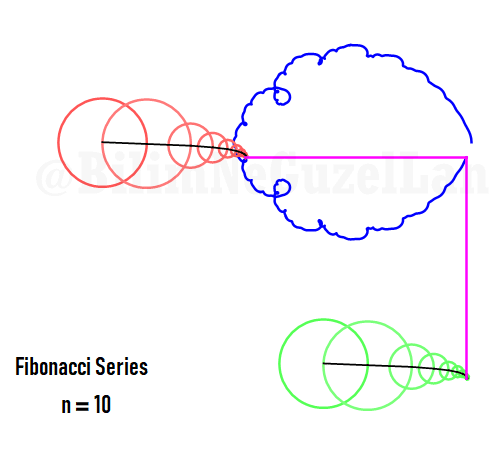
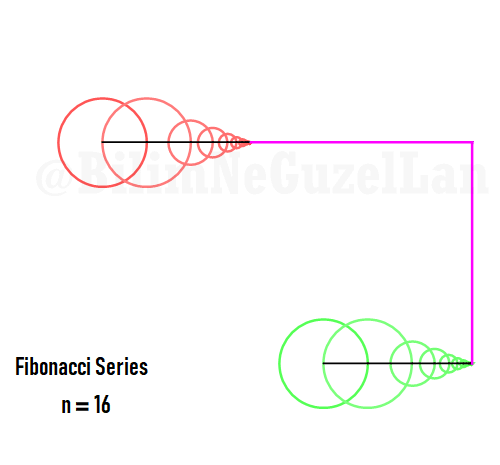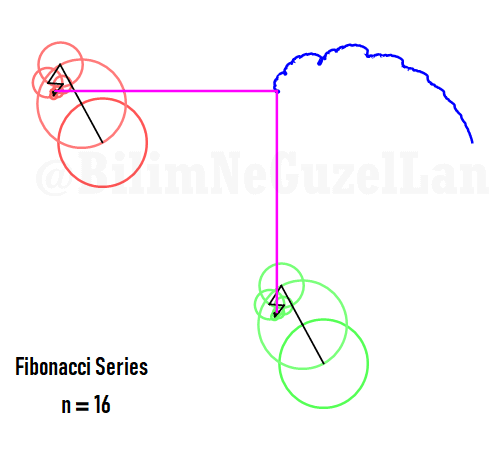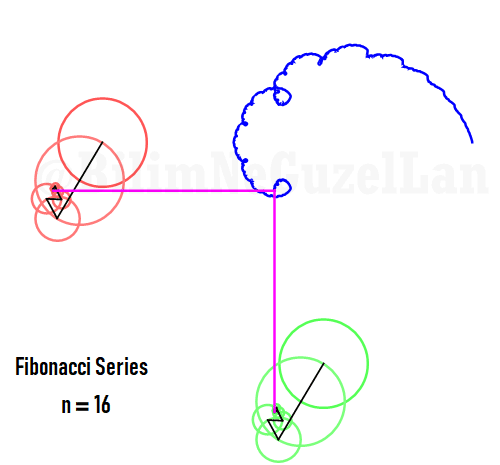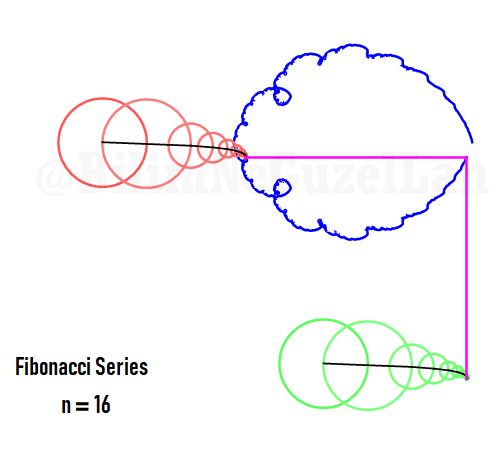
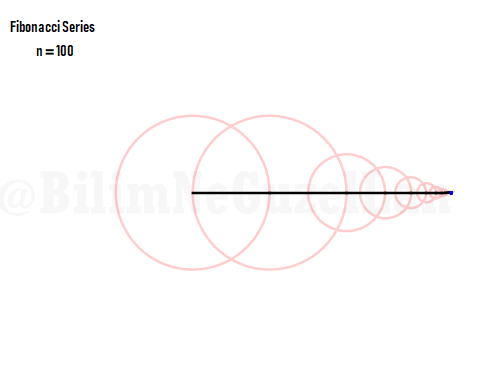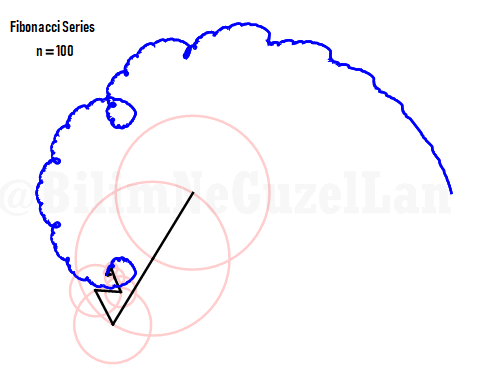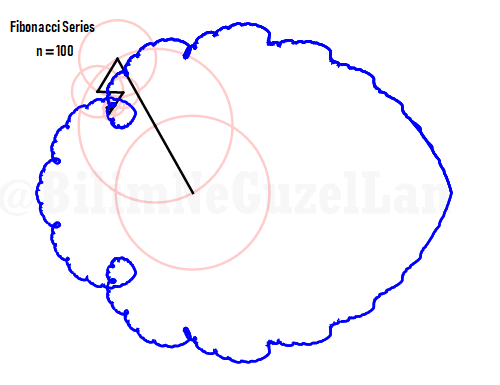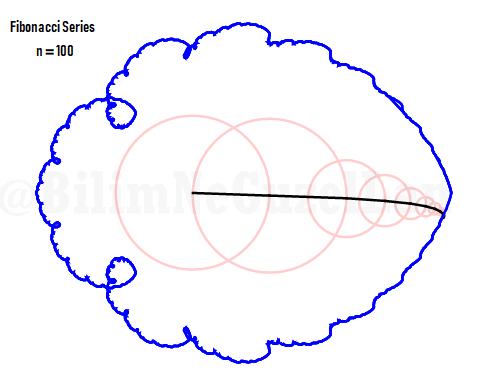
Sekil bir fraktal ve Weierstrass function u gibi görünüyor:

Animasyonlar: Bilgecan Dede

The following two tabs change content below.

• Bilgi
• Son Yazıları

Bilgecan Dede

Hukuğa kafası basmadığından meslek okuluna gitti bu. Ondan sonra gâvur bir ustanın yanına çırak verdiler eli iş tutsun diye, çok şükür ustalığını kazanmış ondan, şimdi de usta olmuş çalışıyor. Eli yüzü düzgün biriyle de evermişler. Ben diyorum, “Bak ileride torun combalak olacak, gel bir şirkette işe başla.” Ama dinlemiyor ki, asi biraz bu.

Yazar: Bilgecan Dede (tümünü gör)

• Fourier Serisi yazısına ek: - 23 Aralık 2018
• Yapay zekâ yüzünden kaybolacak ve eklenecek iş sayıları, bir tabloda - 4 Nisan 2018
• 130 yıl sonra gelen adalet: Telefonun mucidi resmî olarak Antonio Meucci! - 18 Şubat 2018
• Denklem Yazmak - 6 Ocak 2018
• Temel Harmonikler ve Lissajous Eğrileri - 17 Aralık 2017