Temel Harmonikler ve Lissajous Eğrileri

Elinizde bir gitar teli var ve çeşitli notalar çıkarmak istiyorsunuz. Gitar telini yavaşça çektiniz ve bıraktınız. Şöyle bir titreşim olsun:

Telin iki ucu sabit ve tam orta noktası en fazla titreşen yer. Bu titreşime birinci harmonik diyecegiz. Şimdi, gitar telinin bir yerine bastınız ve biraz daha güçlü çektiniz. Şöyle bir titreşim olsun:

Az önceki mavi titreşimi de ekledim. Yeni titreşimimizde bir tane sabit nokta, iki tane de maksimum titreşen nokta var. Bu da ikinci harmoniğimiz. Şimdi, birinci, ikinci ve üçüncü harmoniği koyuyorum:

Asıl göstermek istediğim konuya gelmeden önce, beş harmoniği üst üste koyuyorum. Çünkü çok güzeller (♥ω♥*)

Şimdi, bu üstteki beş harmoniğin grafiğinde mavi eğrilerin kesişimine dikkat edin. En büyük, en yavaş eğrilerin kesişimi. Bu iki eğrinin kesiştiği noktalar aslında dümdüz bir çizgi üzerinde gidiyor. Bu kesiştikleri nokta da kendi çapında bir titreşim hareketi yapıyor. Yalnız, bu nokta bir yüzey üzerinde olduğundan, noktanın iki koordinatı var. Bu iki koordinat da titreşim hareketi yapıyor! Bunu şu şekilde gösterebilirim:

Dikey olarak bir titreşim, ki bu titreşim o kesişim noktasının bir koordinatını belirliyor, yatay olarak da başka bir titreşim var. Bu ikinci titreşim de o kesişim noktasının diğer koordinatını belirliyor. Her hangi bir titreşim şu denklemden bulunabilir:

\(\ddot{x} = -\omega^2 x\)

Bu sadece Newton’un hareket kanunu. \(m\), noktanın kütlesini, \(x\), sadece bir koordinatını, üstündeki iki nokta zamana göre ikinci türevini, \(\omega\) da noktanın ne kadar hızlı titreştiğini gösteriyor (açısal frekans). Sorumuz şu: yukarıdaki gibi iki titreşimi bir araya koyarsak nokta nasıl bir eğri izler? Bu eğri nasıl bulunabilir? Soruyu cevaplamadan önce şunu belirleyelim; eğer bu nokta iki tane titreşimden oluşuyorsa, bu iki titreşim birbirinden tamamen bağımsız olmalı. Mesela, bir titreşim diğerinden farklı hızda olabilir:

Yani iki ayrı denklemin çözümü olmalılar:

\(\ddot{x} = -\omega_x^2 x\)

\(\ddot{y} = -\omega_y^2 y\)

Bu iki denklemi ayrı ayrı çözmemiz gerekiyor. Neyse ki Fransız fizikçi Jules Antoine Lissajous, 1857’de bu denklemi çözmüş.

Denklemi çözmek pek zor değil:

\(x = A_x \sin\left(\omega_x t + \phi_x\right)\)

\(y = A_y \sin\left(\omega_y t + \phi_y\right)\)

Bu Lissajous eğrileri, frekansların oranına \(\omega_x/\omega_y\) ve aralarındaki faz farkına \(\phi_x – \phi_y\) bağlı. Mesela, \(\omega_x/\omega_y = 1\) ise, yani iki titreşimin hızı aynı ise, ilk beklediğimiz gibi düz bir çizgi bunlar. Ancak, titreşim hızlarını aynı tutup aradaki faz farkını değiştirince elips şekilleri veriyorlar. Buraya titreşim hızlarının aynı olup, aradaki faz farkını değiştirdiğim yedi örneği koyuyorum:

Şimdi, \(\omega_x/\omega_y = 2\) olduğu örnekleri koyuyorum:

…ve son olarak, \(\omega_x/\omega_y = 3\):

Devam etmeden önce, Lissajous eğrilerinin özel bir durumu, yani hız farklarının tam sayı olduğu durumlar Chebyshev polinomları olarak biliniyor. Buraya bir kaç tane Chebyshev polinomu koyuyorum:

Evet, gelelim asıl konuya… Lissajous eğrilerini bulmanın kolay bir yolu var mıdır ki? Sonuçta Lissajous eğrileri tamamen soyut kavramlar değiller, çoğu yerde karşımıza çıkabiliyorlar. Eğer bir osiloskop yakınındaysanız, hemen bir girişine 50 Hz AC sinyal, diğerine 60 Hz AC sinyal verin, ekranda Lissajous eğrilerini göreceksiniz.

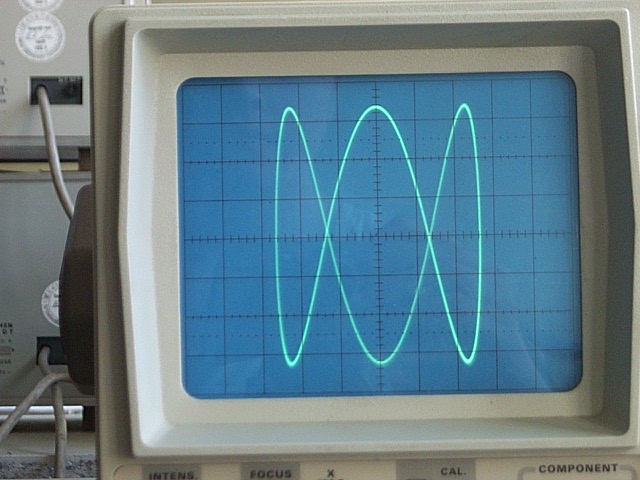
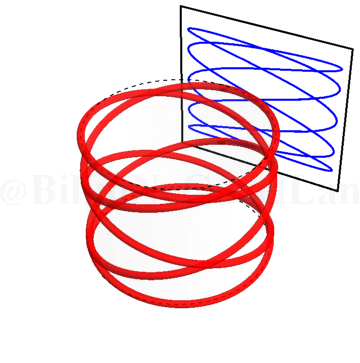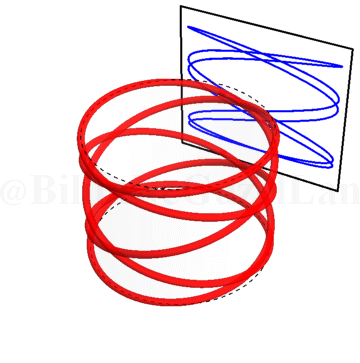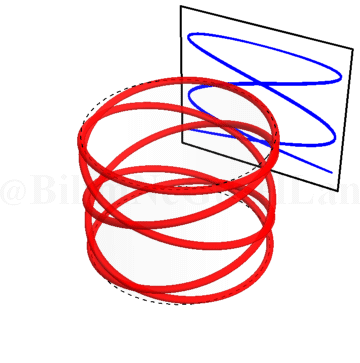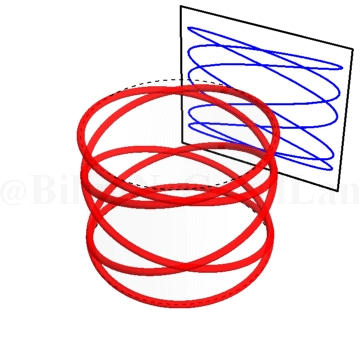
Burası işte Lissajous eğrilerinin daha eğlenceli kısmı 🙂 Bir silindir alın. Silindiri kağıtla kaplayın ve etrafına kendi üzerine kapanan bir sinüs eğrisi çizin. Yani, sinüs eğrisini çizerken başladığınız noktaya geri döneceksiniz. Eğer silindiri şeffaf düşünürseniz, bu sinüs eğrisinin duvara yansıyan gölgesi tam olarak Lissajous eğrilerini veriyor. Silindiri döndürdükçe faz farkını değiştiriyorsunuz. Bu olayı şu şekilde gösterebilirim.

İki frekansın birbirine eşit olduğu durum \(\omega_x/\omega_y = 1\):

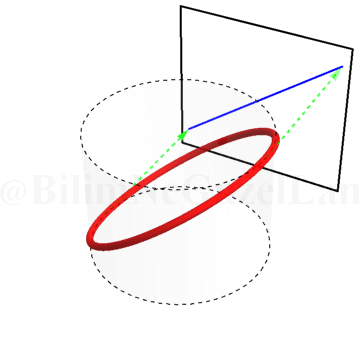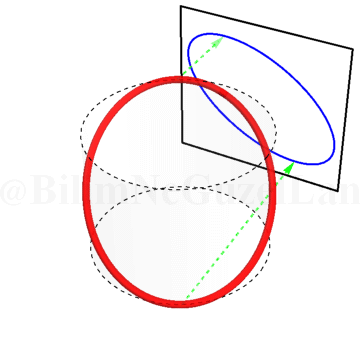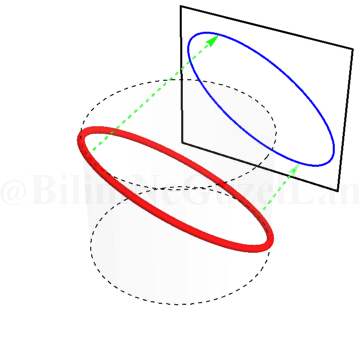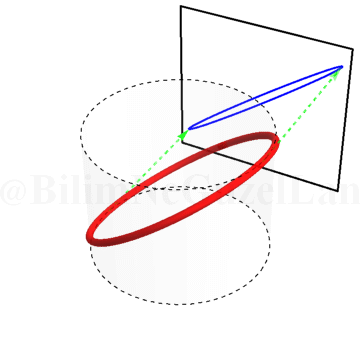
Yeşil okları, gölgeler daha iyi takip edilebilesin diye koydum. Bir yeşil ok eğrinin en yüksek noktasını, diğer yeşil ok eğrinin en alçak noktasını takip ediyor.

\(\omega_x/\omega_y = 2\):

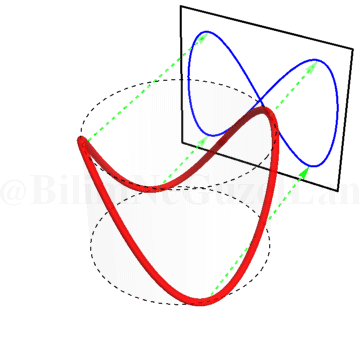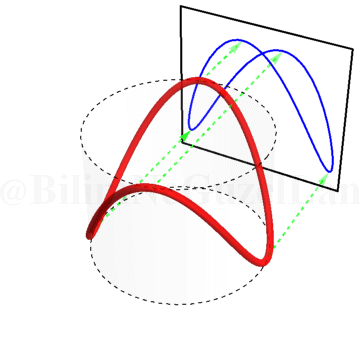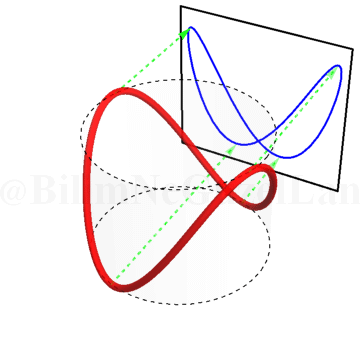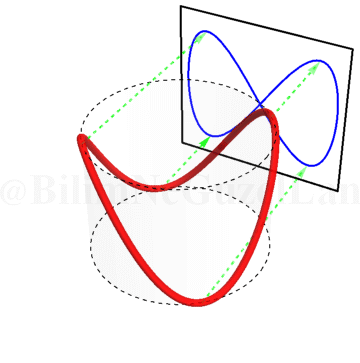
\(\omega_x/\omega_y = 3\):

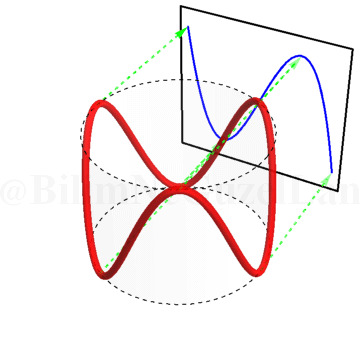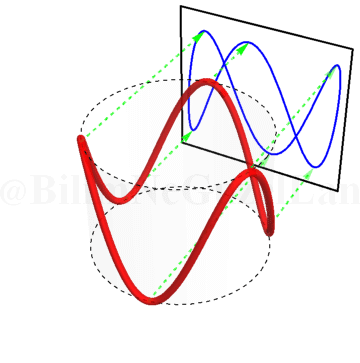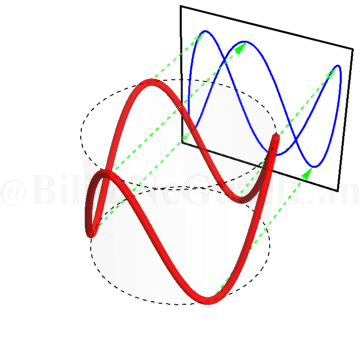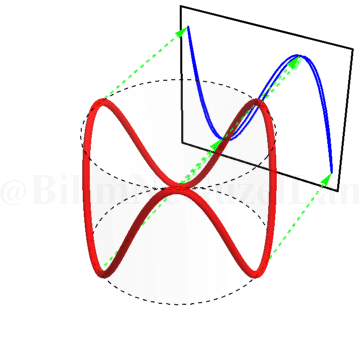
\(\omega_x/\omega_y = 4\):

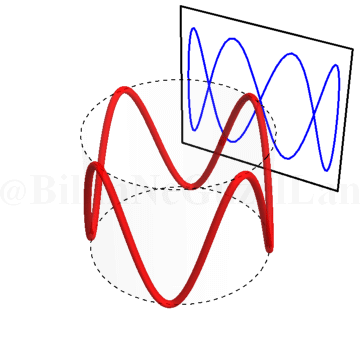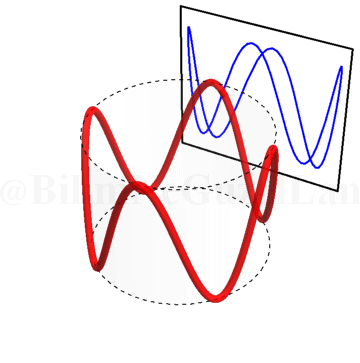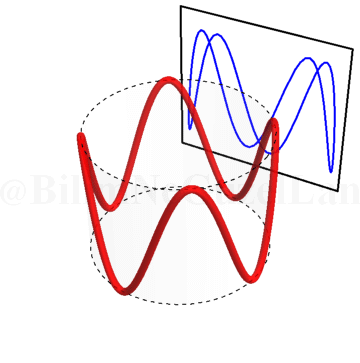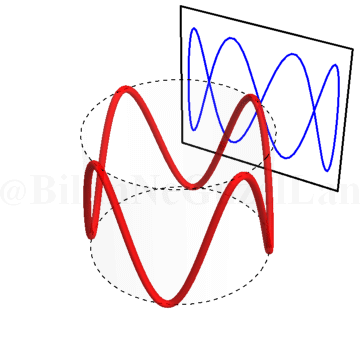
Peki, \(\omega_x/\omega_y\) oranı tam sayı olmazsa Lissajous eğrileri nasıl görünür? Şöyle:

\(\omega_x/\omega_y = 1.25\):

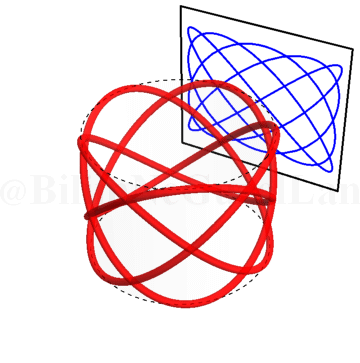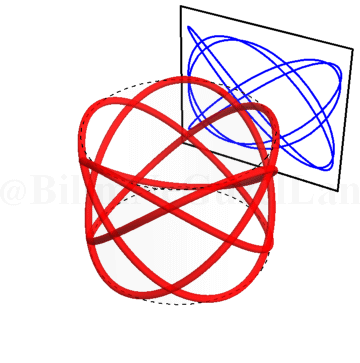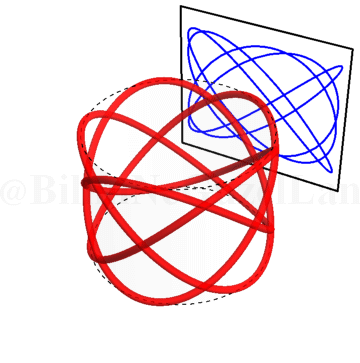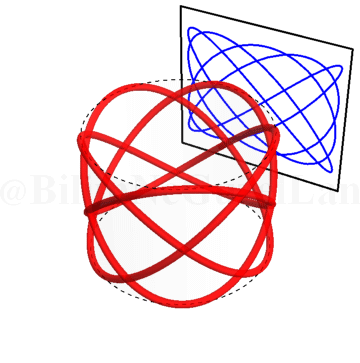
\(\omega_x/\omega_y = 1.5\):

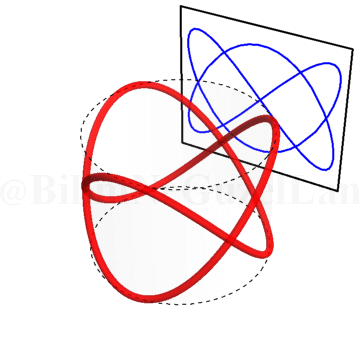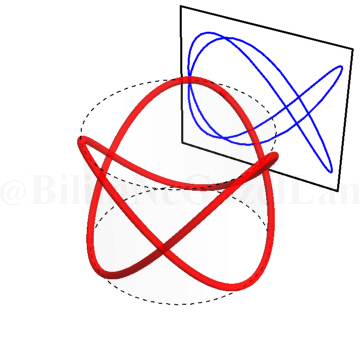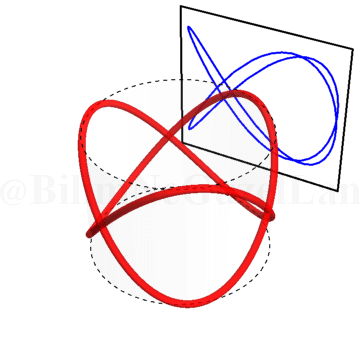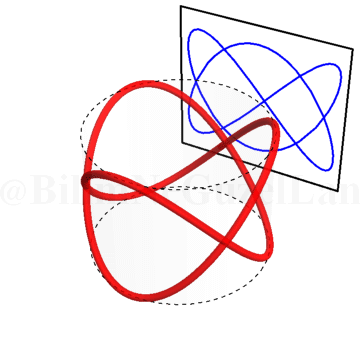
\(\omega_x/\omega_y = 2.25\):

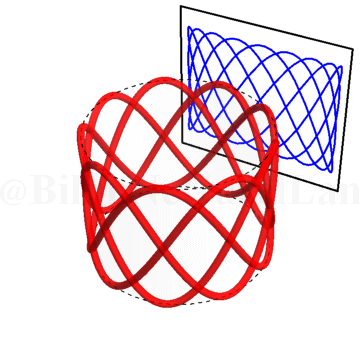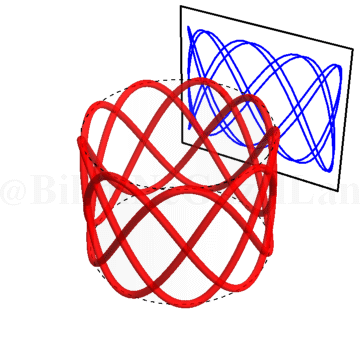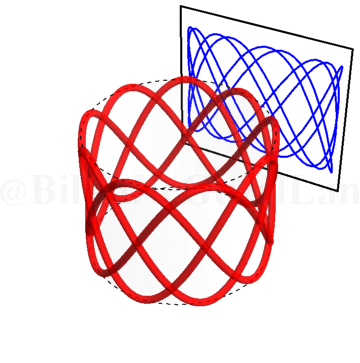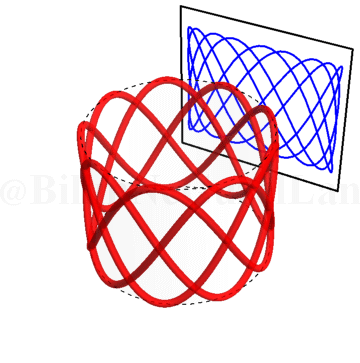
\(\omega_x/\omega_y = 2.5\):

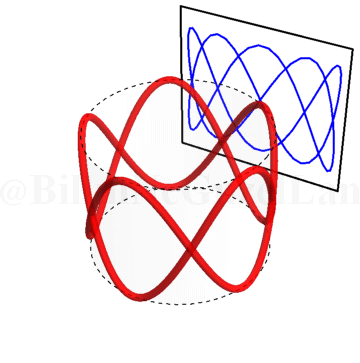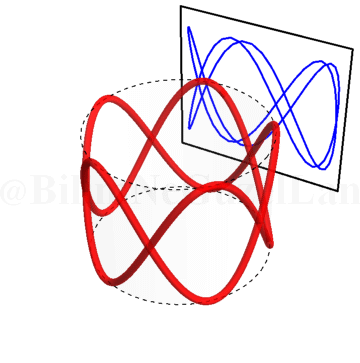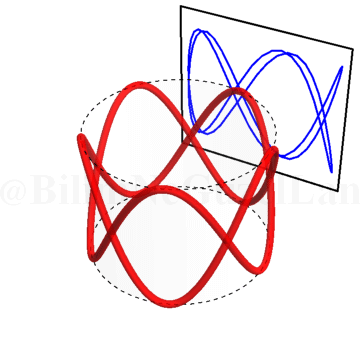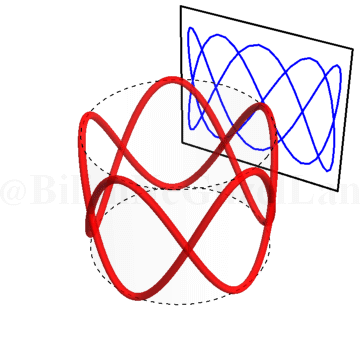
\(\omega_x/\omega_y = 0.25\):

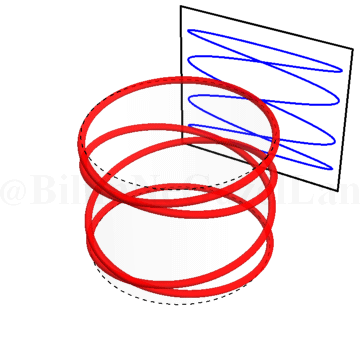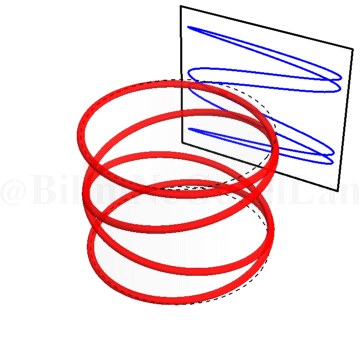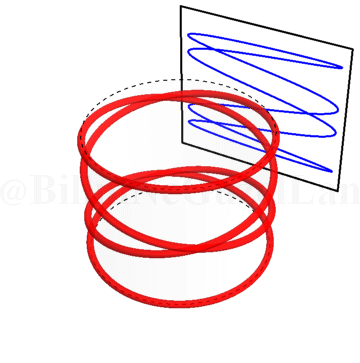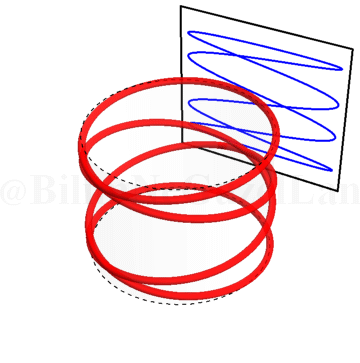
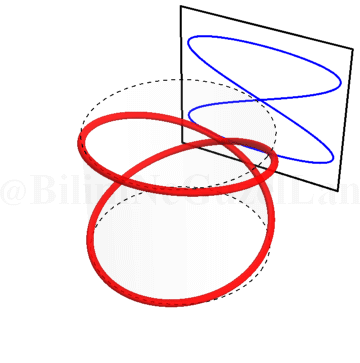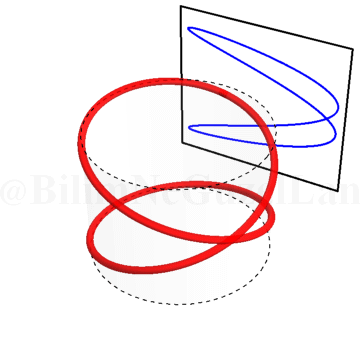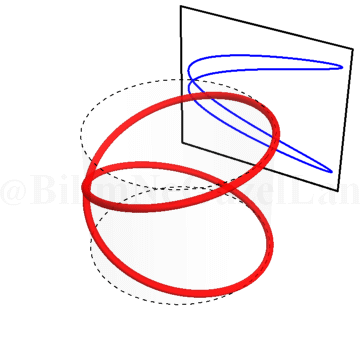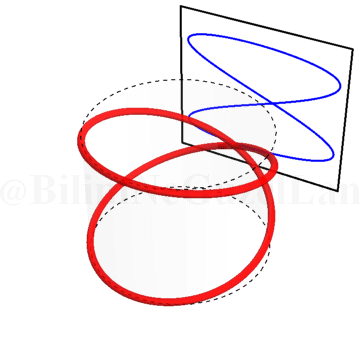
\(\omega_x/\omega_y = 0.4\):

\(\omega_x/\omega_y = 0.5\):

Hemen kendinizin deneyip görebileceğiniz, karmaşık görünen bir olayın bu kadar basit bir açıklaması olması muazzam. Yakınınızda veya okulda bir osiloskop varsa, iki girişini şehir elektriğine takıp hemen deneyin, çabuk! Yok durun! 220 V çok fazla, daha küçük voltajlarla deneyin. Hava sürtünmesinin ve hareketlerinin en az olduğu bir ortamda, bir ipin ucuna ağır, simetrik bir cisim bağlayın ve bu ipi tavana bağlayın. Kısacası bir sarkaç yapın. Sonra, bu sarkacı çekip, bir tarafa itme vererek sallanmasını sağlayın. Cismin izlediği yol Lissajous eğrilerinden biri olacak.

Yazı ve animasyonlar: Bilgecan Dede.

The following two tabs change content below.

• Bilgi
• Son Yazıları

Bilgecan Dede

Hukuğa kafası basmadığından meslek okuluna gitti bu. Ondan sonra gâvur bir ustanın yanına çırak verdiler eli iş tutsun diye, çok şükür ustalığını kazanmış ondan, şimdi de usta olmuş çalışıyor. Eli yüzü düzgün biriyle de evermişler. Ben diyorum, “Bak ileride torun combalak olacak, gel bir şirkette işe başla.” Ama dinlemiyor ki, asi biraz bu.

Yazar: Bilgecan Dede (tümünü gör)

• Fourier Serisi yazısına ek: - 23 Aralık 2018
• Yapay zekâ yüzünden kaybolacak ve eklenecek iş sayıları, bir tabloda - 4 Nisan 2018
• 130 yıl sonra gelen adalet: Telefonun mucidi resmî olarak Antonio Meucci! - 18 Şubat 2018
• Denklem Yazmak - 6 Ocak 2018
• Temel Harmonikler ve Lissajous Eğrileri - 17 Aralık 2017