Kökler

Bu yazıda, basit ve kısa bir konudan bahsedeceğim. Liseden, ikinci derece polinomun köklerini bulmayı biliyoruz, kuadratik formül:

\(a x^2 + b x + c = 0\)

\(a,b,c\)’yi biliyorsak \(x\)’i bulmak gayet kolay:

\(x_{1,2} = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a}\)

Mesela, \(x^2 + x + 1 = 0\) için, iki tane kokumuz var:

\(x_{1,2} = -(-1)^{1/3}, (-1)^{2/3}\),

ya da

\(x_{1,2} = -0.5 \pm 0.86025 i \).

Bunu görselleştirirsek,

Üçüncü dereceden polinomumuz varsa ne yapacağız? Biraz daha meşakkatli de olsa elimizde kökleri bulmak için aletimiz halen var. Mesela, \(x^3 + x + 1 = 0\)’in kökleri üç tane;

\(x_{1,2,3} =  0.341164 + 1.16154 i , -0.682328 , 0.341164 – 1.16154 i \)

Tekrar görselleştirirsek;

Dördüncü derece polinomun dört kökünü bulmak için de çok daha karmaşık bir formül de olsa, yine bu şekilde köklerini bulacağım bir formül var. Beşinci derece ve daha büyük dereceli polinomlar için Niels Abel’in gösterdiği üzere, bir formülümüz olamaz. Bu denklemi numerik olarak çözmek zorundayız. 

Şimdi, şu işi biraz karmaşıklaştıralım. Çünkü görseller çok eğlenceli (・∀・). Önce, çözmemiz gereken denklem ikinci derece bir polinom olsun, ama bir terim (z) ekleyeyim:

\(x^2 + x z + 1 = 0\)

Eğer \(z = 1\) ise kökleri yukarıda. Şimdi, z’yi birim çember etrafında dondurup köklerine bakmak istiyorum:

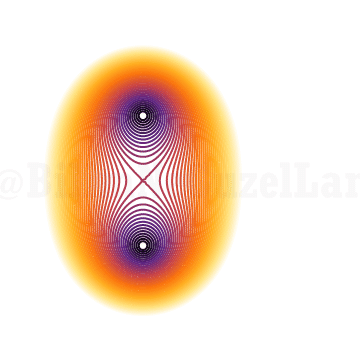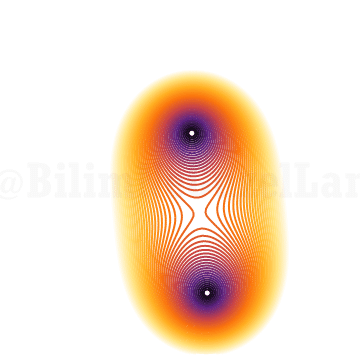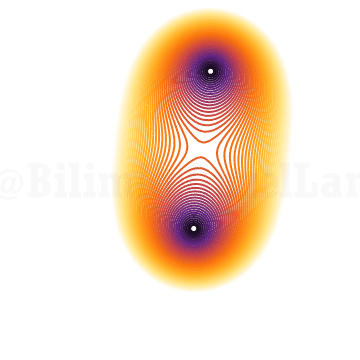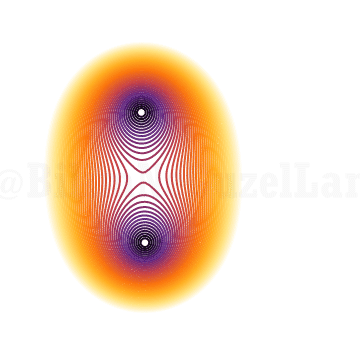
İki mor nokta benim köklerimi gösteriyor. z’yi birim çember etrafında dondurup köklerine bakarsam kökler bu şekilde davranıyor. Henüz pek eğlenceli değil. Üçüncü derece denkleme bir bakayım:

\(x^3 + x z + 1 = 0\)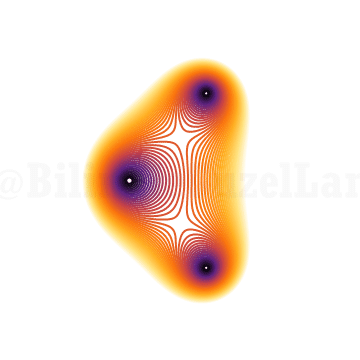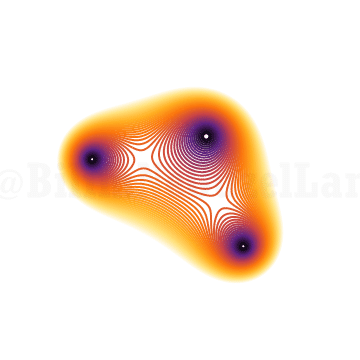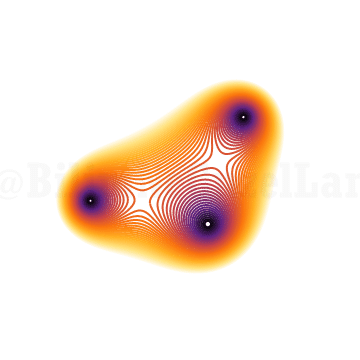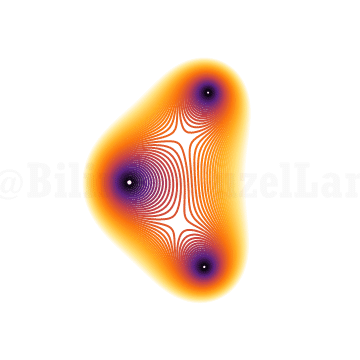

Hmm, biraz güzel görünmeye başladı. Tekrar, z’yi birim çember etrafında donduruyorum sadece. Dördüncü derece polinom?

\(x^4 + x z + 1 = 0\)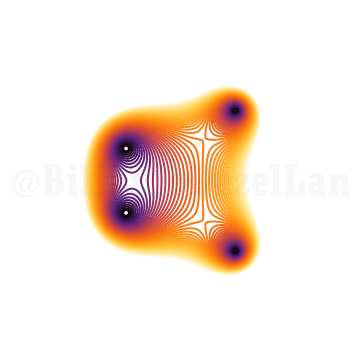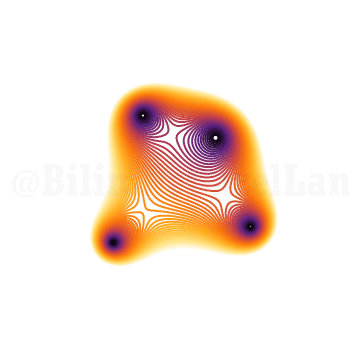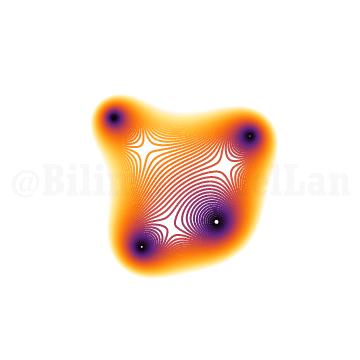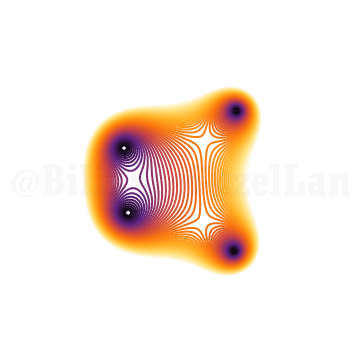

\(x^5 + x z + 1 = 0\)

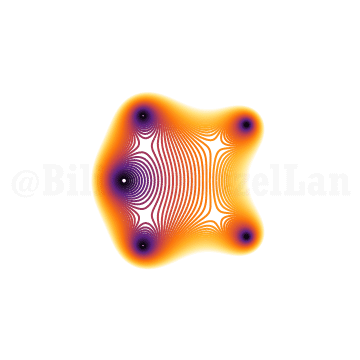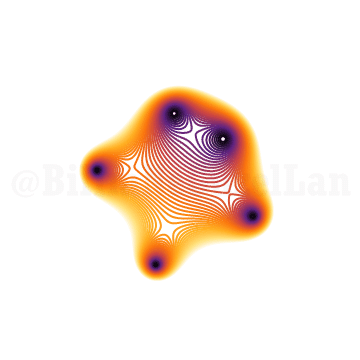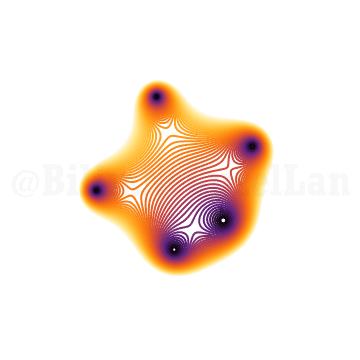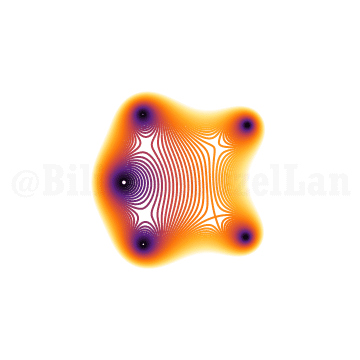
\(x^6 + x z + 1 = 0\)

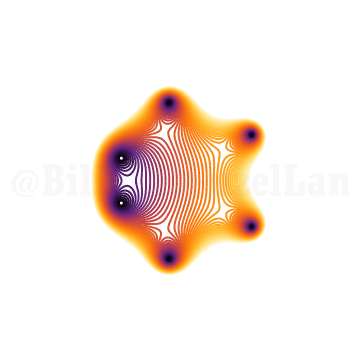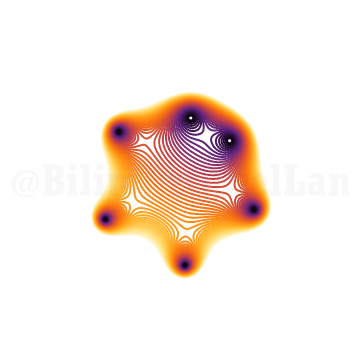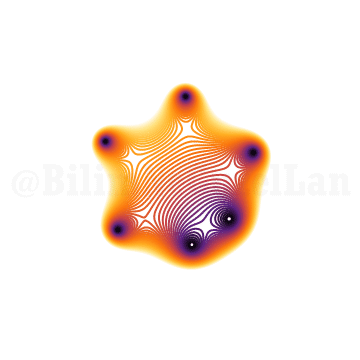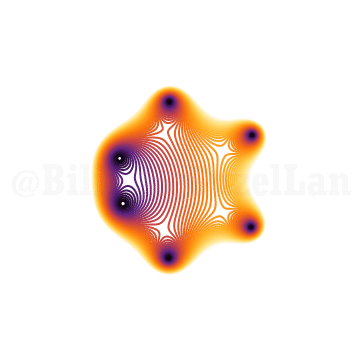
Dereceyi arttırdıkça (16. derece) şöyle bir şey karşıma çıkıyor:

\(x^{16} + x z + 1 = 0\)

Uuuu daha da arttır bebeyim:

\(x^{25} + x z + 1 = 0\)

\(x^{25} + x^2 z + 1 = 0\)

\(x^{25} + x^4 z + 1 = 0\)

Önceki polinomlara dönüp köklerin nasıl değiştiğini göstermek istiyorum:

\(x^{5} + x^2 z + 1 = 0\)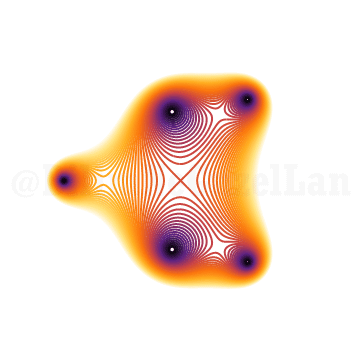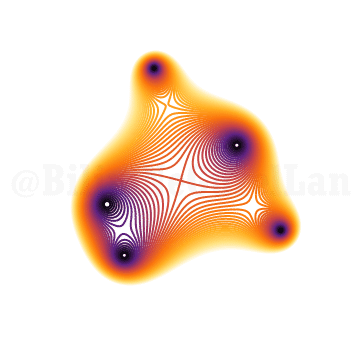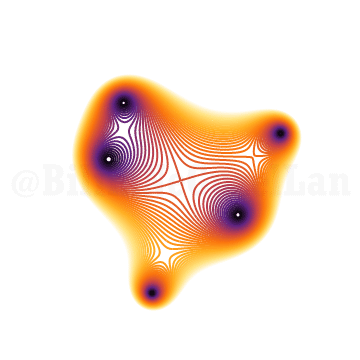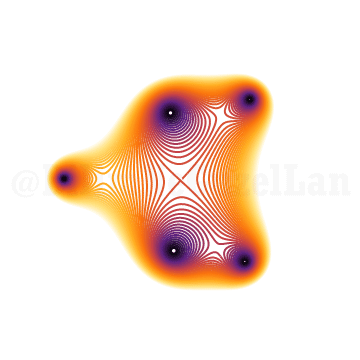

\(x^{5} + x^3 z + 1 = 0\)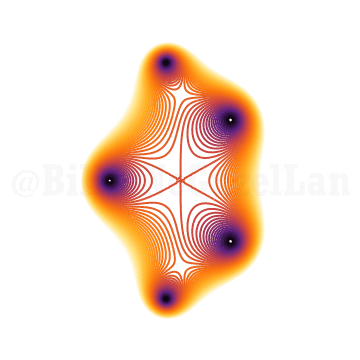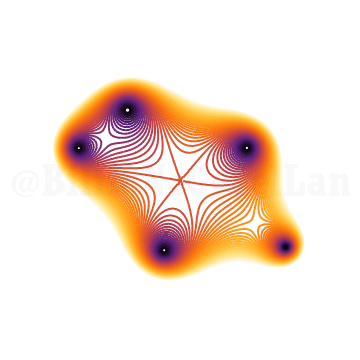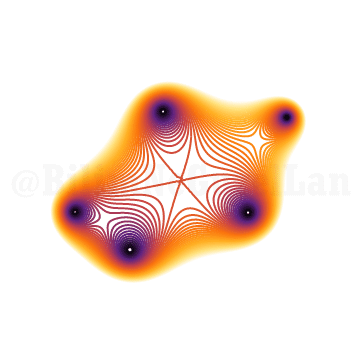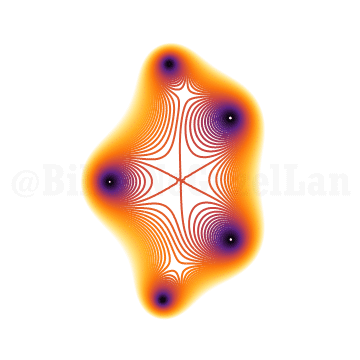

\(x^{5} + x^4 z + 1 = 0\)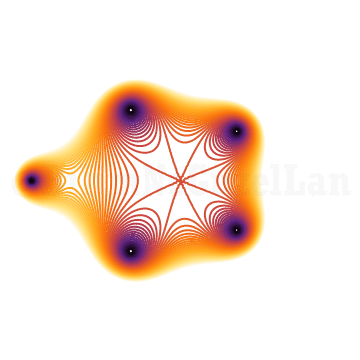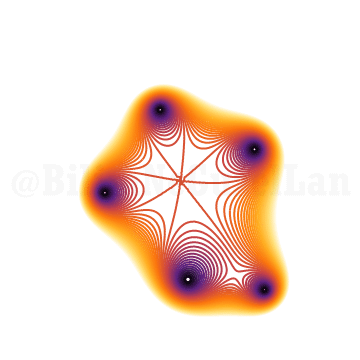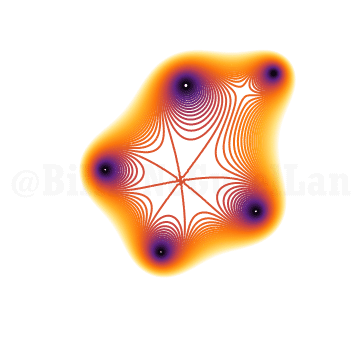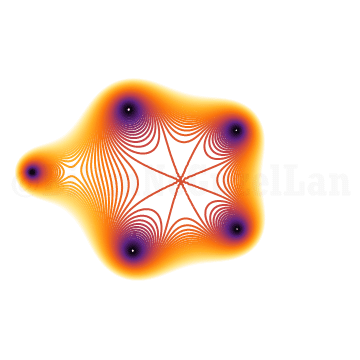

\(x^{5} + x^3 + x^2 z + 1 = 0\)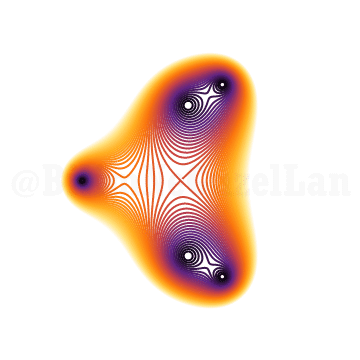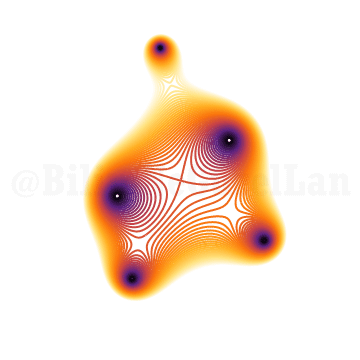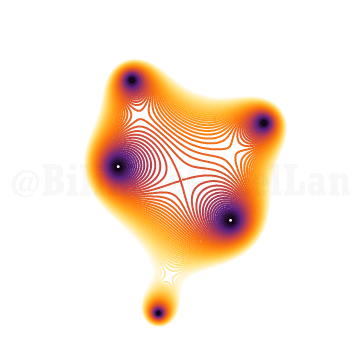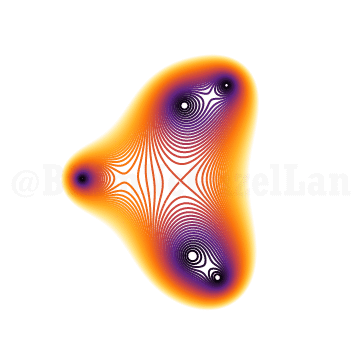

Çok karmaşık bir problemin çözümünü görselleştirince anlaması daha kolay değil mi?

Yazı ve animasyonlar: Bilgecan Dede

The following two tabs change content below.

• Bilgi
• Son Yazıları

Bilgecan Dede

Hukuğa kafası basmadığından meslek okuluna gitti bu. Ondan sonra gâvur bir ustanın yanına çırak verdiler eli iş tutsun diye, çok şükür ustalığını kazanmış ondan, şimdi de usta olmuş çalışıyor. Eli yüzü düzgün biriyle de evermişler. Ben diyorum, “Bak ileride torun combalak olacak, gel bir şirkette işe başla.” Ama dinlemiyor ki, asi biraz bu.

Yazar: Bilgecan Dede (tümünü gör)

• Fourier Serisi yazısına ek: - 23 Aralık 2018
• Yapay zekâ yüzünden kaybolacak ve eklenecek iş sayıları, bir tabloda - 4 Nisan 2018
• 130 yıl sonra gelen adalet: Telefonun mucidi resmî olarak Antonio Meucci! - 18 Şubat 2018
• Denklem Yazmak - 6 Ocak 2018
• Temel Harmonikler ve Lissajous Eğrileri - 17 Aralık 2017