Banu Alkan’ı Kültür Bakanı yapıyoruz (k-means algoritması)
Bu yazımızda veri analizi, makine öğrenmesinde temel bir kavramdan bahsedeceğim; k-means kümelenmesi (k-means clustering).
Elinizde bir takım veriler var. Mesela şöyle 5 tane veri:
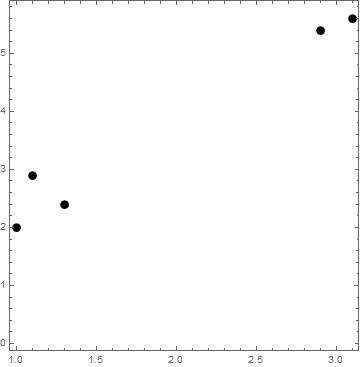
Bu 5 verinin ikişer tane bileşeni var (x,y). Bu veriler birçok şeyi gösterebilir, mesela bir mahalledeki beş evin boyu, ücreti; önünüzdeki beş bilgisayarın RAM’i, işlemci hızı… Aklınıza gelen, iki bileşene sahip herhangi bir şey. Ancak normalde iki bileşene sahip olmak zorunda değiller. Yazımda, basitleştirmek için iki bileşen ile çalışacağım.
Amacımız bu verileri kümelemek. Bu yukarıdaki beş noktaya baktığınızda bir insan için kümelemek çok zor değil, 3 nokta bir yere, 2 nokta bir yere kümelenmiş. Mesela, bunlar önünüzdeki beş bilgisayarın (RAM, CPU) özellikleriyse bu kümeler size şunu anlatıyormuşmuş: elinde üç tane 1990’lardan kalma eski bilgisayar var, iki tane de yeni, hızlı bilgisayar var.
Ama bu kümeleme problemini bir bilgisayara nasıl öğretebilirsiniz? Bilgisayar bu elinizdeki beş noktadan üç tane eski, iki tane yeni bilgisayar olduğunu nasıl anlayabilir?
Makine öğrenmesinde (machine learning – bunu da makine öğrenmesi diye çevirmeyi sevmiyorum) bilgisayara bu verileri ayırmak için birçok yöntem var. En basitlerinden biri, k-means. Bugün bundan bahsedeceğim.
Machine learning algoritmalarına başlamadan önce, Banu Alkan’dan biraz bahsetmek istiyorum.
Banu Alkan, 2007’deki bir röportajında, Kültür Bakanı olmak istediğinden bahsetmiş. Videosu da burada:
Banu Alkan diyor ki (videoda 12:09):
“Mutlaka bu ülkeye, bir gün, siyasette olacağımı ve bu ülkede Kültür ve Turizm Bakanı olacağımı, her zaman ve yalnızca ve yalnızca Kültür ve Turizm Bakanı olmak istiyorum ama bir milletvekilliğinden sonra tabii inşallah.”
k-means’de (ve diğer kümeleme algoritmalarında) temelde yapmaya çalıştığımız şey Banu Alkan’ın yapmaya çalıştığı şey ile benzer: muhtar/bakan seçmeye çalışıyoruz. Bu verilere birkaç tane muhtar atayacağız. Bu noktalar muhtarlarını seçecekler.
Mesela, şöyle bir mahallemiz olsunmuş:
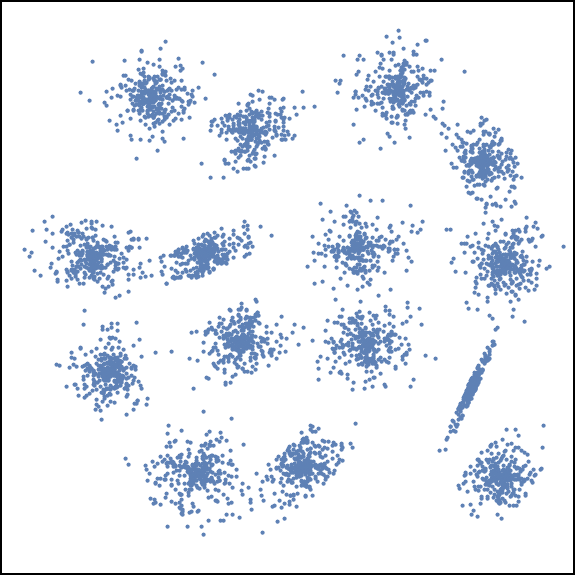
Her bir nokta bir seçmen olsunmuş. Banu Alkan buraya Kültür Bakanı olmak istiyor. Herkese eşit mesafede, adil olmak ve herkesin sorunlarını eşit olarak dinlemek istiyor. Bu yüzden mahalleye yeni giren Banu’ya şöyle bir şey diyoruz:
0) Önce kaç aday olacağına karar ver, seçmenleri bu kadar kümeye ayıracağız.
1) Rastgele bir yerden başla.
2) Sana en yakın seçmenleri kendine ata, bu seçmenler sana oy verecekler. Başka bir adaya yakın olan seçmenleri de diğer adaya ata, bu diğer seçmenler de diğer adaylara oy verecekler.
3) Sana atanmış olan seçmenlerin tam ortasına geç, diğer aday da diğer seçmenlerin tam ortasına gecsin.
4) Artık yerin değişmeyene kadar, 1’inci aşamaya geri dön ve bunu tekrarla.
Banu Alkan, zeki bir insan. Kendisine bu algoritmayı verirsek seçimi kazanacağından kuşkumuz yok.
Bir centroid atıyoruz: \(\mu_k\), bu centroid, bir kümenin tam orta noktası. \(k\), centroid’in indisi, \(\mu_k\) de bu mahellede bir koordinat belirliyor. Eğer \(K\) tane Banu varsa, \(k\), 1’den \(K\)’ya kadar değerler alabilir. Sonra, her bir verinin centroid’e uzaklığını ölçüyoruz. Bunu ölçmek için Pisagor bağıntısını kullanıyoruz. Eğer i’nci noktanın koordinatı \((x_i, y_i)\) ise, her bir centroid (\(k\)) için şunu hesaplıyoruz:
\(d_i^2 = \left(x_i – (\mu_x)_k \right)^2 + \left(y_i – (\mu_y)_k \right)^2 \)
Bu veri, artık en yakın centroid’e bağlı. Sonra da, centroid’i bu bir kümede olan verilerin aritmetik ortalamasına koyuyoruz ve tüm işlemi tekrar ediyoruz.
Banu Alkan, tek başına geliyor. Ama yanında başka bir aday yok. Sadece bir tane. Seçmenler hemen Banu’yu ortalarına alıyorlar ve omuzlarda taşınıyor Banu:
Banu nereden başlarsa başlasın hep aynı yere geliyor. Bu animasyonda üç kere rastgele yerlerden başlattım. Her seferinde, bie iterasyondan sonra hemen tam ortaya geçti.
Şimdi iki tane Banu var. Banu hareketi ikiye bölünmüş. İki Banu (vaatler, kişilikler tamamen aynı, niye bölünmüşler ki) aynı yere geliyorlar. 10-11 iterasyondan sonra iki Banu da seçmenleri eşitçe paylaşıyor.
Kırmızı seçmenler ve mavi seçmenler var.
Şimdi Banu onurlu mücadelesi üçe bölündü. Üç Banu da mahalleye geliyorlar ve yarışıyorlar. Dört beş iterasyondan sonra her Banu bir küme tarafından seçilmiş oluyor. Bu Banu’lar tüm seçmenlere olabilecek en eşit mesafedeler.
Dört Banu ile,
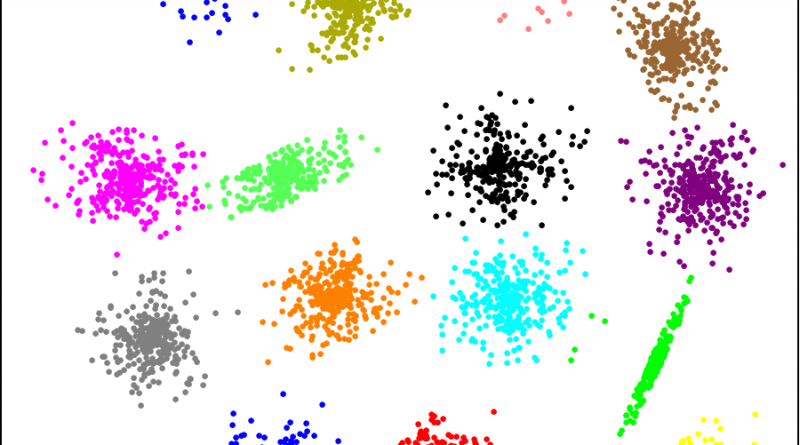
…ve… Mahallede on beş tane küme var. On beş tane Banu’yu seçimde yarıştırırsak her bir kümeye bir Banu düşer mi? Pek değil. Banuların son yeri, Banuların başlangıç yerlerine çok bağımlı. Bakın, iki tane örnek koyuyorum. İki örnekte de Banular tamamen rastgele yerlerden başlıyorlar.
Ancak, Banuların son yeri başlama noktalarına bağlı. Mesela, şu örnekte Banular seçmenleri paylaşmak için bayağı uğraşıyorlar:
On beş Banu’yu, on beş kümeye ayırmak için baştan birkaç şey bilmemiz gerekiyor: On beş tane küme olacağı ve bu kümelerin yaklaşık yerleri. Ölme eşeğim ölme diyorsunuz, evet k-means’in handikapı bu. On beş Banu’yu, kümelere yakın yerlerden ben başlatırsam, hepsi çabucak kümelere sahip çıkıyorlar:
Ayrıca en son kümeleşme çok keskin değil. Bazı noktalar yanlış atanmış gibi. k-means, şu örnekte de pek başarısız:
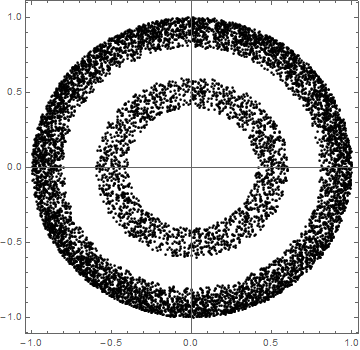
Bu noktaları k-means ile kümelemeye çalışırsanız iki kümenin ortasının iki çemberin merkezi olma ihtimali var.
Ama, k-means çok basit ve yukarıdaki koşullar sağlandığı sürece iş görüyor. Eğer internet kullanıyorsanız, çok büyük olasılıkla k-means ile yazılmış en az bir algoritma kullanıyorsunuz. Bir kullanım alanını resim sıkıştırma olarak gösterebilirim. Bu grafikte, soldaki galaksi fotoğrafını k-means ile birkaç renge sıkıştırdım.

Daha iyi kümeleme algoritmaları, makine öğrenmesi algoritmaları, noral ağ algoritmaları için beklemede kalın.
Yazı ve tüm görseller: Bilgecan Dede.
Banu Alkan’ın mahallesi buradan.
Doga Kurkcuoglu
Yazar: Doga Kurkcuoglu (tümünü gör)
- Fourier Serisi yazısına ek: - 23 Aralık 2018
- Yapay zekâ yüzünden kaybolacak ve eklenecek iş sayıları, bir tabloda - 4 Nisan 2018
- 130 yıl sonra gelen adalet: Telefonun mucidi resmî olarak Antonio Meucci! - 18 Şubat 2018
- Denklem Yazmak - 6 Ocak 2018
- Temel Harmonikler ve Lissajous Eğrileri - 17 Aralık 2017