Where the hell is 1/3, or Introduction to Chaos
This article is translation of our Turkish article with the same name.
For another article about Mandelbrot and Julia Set, refer to our other article (to be translated soon).
Chaos is a relatively new branch of mathematics. The verb chaos means “disarray” in Greek.
Let me try to expand the chaos concept.
Now, have a loud, intense cough. You have just made a tiny ripple in the atmosphere. You inhaled and exhaled some air. You might not observe this small effect on the atmosphere today or tomorrow. However your intense cough might yield a typhoon that devastates the houses in Bangladesh after one year. Maybe… Who knows… You cannot even predict the effect of a butterfly after ten years.
Thus, the meteorology discipline can only make one week prediction, not one year.
The very close initial conditions can yield very distant situations after a long time.
Now, the chaos theory just deals just with this problem.
Is there such chaos/disarray in mathematics? Indeed there is, so much so there is a whole theory named after it!
In this article, I will give an example from chaos in mathematics.
Have you ever wondered where exactly is 1/3? We will try to find where is 1/3.
We know that 1/3 is a number between zero and one, meaning in [0, 1] interval.
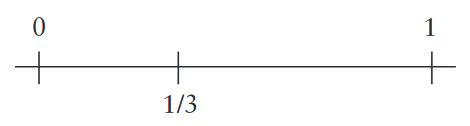
But knowing this information does not mean that we know where the hell is 1/3. Let us try to understand better where is 1/3.
If we divide the interval [0, 1] to exact half, where does the 1/3 fall? Right? Left? That is, is 1/3 smaller or bigger than 1/2? Of course 1/3 < 1/2 inequality is valid and 1/3 falls to the interval on the left.
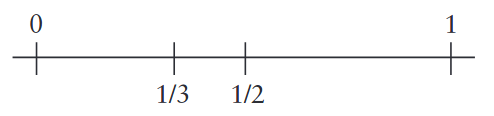
In the figure above, we divided the [0, 1] interval by half and obtained [0, 1/2] ve [1/2, 1] intervals. We can see that 1/3 is in [0, 1/2] intervals, so those inequalities involving 0 1/3 1/2 are valid. Now divide the [0, 1/2] interval by half of which 1/3 sits: we obtained
[0, 1/4] and [1/4, 2/4]
intervals. Of which of these intervals does 1/3 falls into? Right or left? Since 1/4 1/3 2/4 inequalities are valid, 1/3 falls into second interval, that is, [1/4, 2/4] interval on the right.
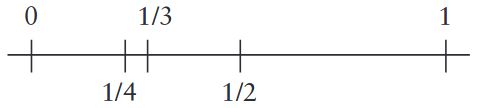
Now divide [1/4, 2/4] interval by half. We obtained
[2/8, 3/8] and [3/8, 4/8]
intervals. Since 2/8 < 1/3 < 3/8 inequalities are valid, 1/3 falls into the first interval on the left.
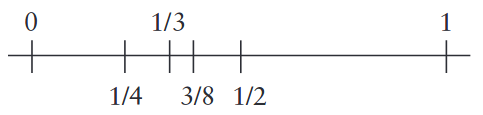
What if you divide [2/8, 3/8] interval by half? And continue to divide the intervals like this?
In general, if you divide the interval [0, 1] to 2n equal length intervals, to which interval does the 1/3 fall into?
Let me give you the answer: the number 1/3 falls into alternating left and right of those equally divided intervals. Meaning that, it falls into left of 1/2, right of 1/4, left of 3/8, right of 6/16…
But, where is the chaos here?
We know the equality 1/3 = 0.333333… 0.333333 number is very close to 1/3, but is not 1/3. Like 1/3, 0.333333 falls into alternating left and right, but its behavior diverges completely from that of 1/3, as if it is completely independent of 1/3. Now, that is the chaos. Two similar numbers behave likewise initially, but one gives no clue about the another after a while.
Let’s turn back to our search for 1/3. Below we present these identities, but it is not difficult to check if the identities that we skipped here are correct or not:
for any value of n, there is an integer an such that,
an/2n ≤ 1/3 ≤ (an+1)/2n (1)
inequalities are valid. As you can infer from above,
a1= 0
a2= 1
a3= 2
a4= 5
a5= 10
a6= 21
a7= 42
expressions are valid. It is not hard to find the subsequent numbers. Well, the array goes like this: 0, 1, 2, 5, 10, 21, 42, 85, 170, 341, 682… The reader can predict what the next elements of this array. However, a prediction is only a, well, prediction. This predictions needs to be proven.
Now, we will prove the statements:
If n is odd, an is even
If n is even, an is odd.
Before diving into the calculations, we have to prove that there cannot be any equality in the inequalities of (1) above. Indeed, for an integer a, if a/2n = 1/3 , 3a= 2n is also true, thus we can deduce that 3 divides 2n, which is incorrect. Therefore we can write the inequalities at (1) in a more precise way,
an/2n < 1/3 < (an+1)/2n .
Let’s save those inequalities from their denominators and multiply those numbers by 3 x 2n . We obtain:
3an < 2n < 3an+3
inequalities. Therefore the number 2n is bigger than 3an, but smaller than 3an+3. There are two numbers that are bigger than 3an and smaller than 3an+3: 3an+1 ve 3an+2. Consequently the number 2n is equal to one of those numbers:
Either 2n= 3an+1 or 2n= 3an+2. (2)
Which one of these is true? The answer depends on if n is odd or even. If n is even 2n= 3an+1, where is if odd 2n= 3an+2. Why? I will tell you why in a minute. First we need some preliminaries.
This needs to be known: 2n-2, 2n-1 and 2n are three consecutive numbers. This means that one of these has to be divided by three. Since 2n cannot be divided by 3, we can understand that one and only one of the 2n-2 and 2n-1 numbers can be divided by three.
Claim: If n is even, 2n-1 is divided by three. If n is odd, 2n-2 is divided by three.
Proof: First assume that n is even and write the n as 2m:
n= 2m.
Since 2m-1, 2m and 2m+1 are consecutive numbers, one of them is divided by three. But of course 2m is not the one. It means that one of these 2m-1 and 2m+1 numbers is divided by three. Keep this in mind, it will be required in the next paragraph.
Now let’s carry out this simple calculation:
2n-1 = 22m-1 = (2m)2-1 = (2m-1)(2m+1).
We have already learned that one of the numbers 2m-1 ve 2m+1 on the right hand side of the equation can be divided by three. So their product, 2n-1, is divided by three. We have proven the first part of our claim.
Now assume that n is an odd number and write n= 2m+1. Let’s calculate this again:
2n-2 = 22m+1-2 = 2(22m-1).
Hmm, did not we learn that 22m-1 is divided by three? Thus the numbers in the equation above can be divided by three, 2n-2 is divided by three.
Our claim is proven.
Now, let’s go back to (2).
If 2n= 3an+1 equality is true, so is 3an= 2n-1. This means 2n-1 is divided by three (and 2n-2 is not divisible by three). From the claim above, it is clear that n is even.
If 2n= 3an+2 equality is true, 3an= 2n-2 is also true, meaning that 2n-2 is divided by three (and 2n-1 is not divisible by three). And from the claim above, we understand that n is odd.
This means we have proven,
If n is even, 2n= 3an+1
If n is odd, 2n= 3an+2
propositions. Namely we have proven,
If n is even, an= (2n-1)/3
If n is odd, an= (2n-2)/3
propositions. Yaay!
Now let’s investigate if an is even or odd.
If n is even, meaning if an= (2n-1)/3, an cannot be divided by two, since 2n-1 cannot be divided by two. This means an is odd.
If n is odd, meaning if an= (2n-2)/3 = 2(2n-1-1)/2, of course an is divided by two.
All these hassle means that 1/3 falls into alternating left and right of the intervals.
Lastly, let’s prove the following beautiful equation:
1/3 = 1/2-1/4+1/8-1/16+1/32-1/64+… (3)
The summation on the right hand side of the equation is an infinite summation. Let’s call the infinite sum, x :
x= 1/2-1/4+1/8-1/16+1/32-1/64+…
Now multiply the x by two :
2x = 2(1/2-1/4+1/8-1/16+1/32-1/64+1/128-1/256+…)
= 1-1/2+1/4 –1/8+1/16-1/32+1/64 –1/128+…
= 1-(1/2 –1/4+1/8-1/16+1/32-1/64+1/128-…)
= 1-x.
So 2x = 1-x. And we easily find that x= 1/3 !
The equation (3) is proven.1
If this proof did not convince you for the validity of equation (3), try it yourself:
1/2 = 0,5
1/2–1/4 = 0,25
1/2–1/4+1/8 = 0,375
1/2–1/4+1/8–1/16 = 0,3125
1/2–1/4+1/8–1/16+1/32 = 0,3475
1/2–1/4+1/8–1/16+1/32–1/64 = 0,328125
1/2–1/4+1/8–1/16+1/32–1/64+1/128 = 0,3359375
1/2–1/4+1/8–1/16+1/32–1/64+1/128–1/256 = 0,33203125
1/2–1/4+1/8–1/16+1/32–1/64+1/128–1/256+1/512 = 0,333984375
1/2–1/4+1/8–1/16+1/32–1/64+1/128–1/256+1/512–1/1024 = 0,3330078125
1/2–1/4+1/8–1/16+1/32–1/64+1/128–1/256+1/512–1/1024+1/2048 = 0,33349609375
1/2–1/4+1/8–1/16+1/32–1/64+1/128–1/256+1/512–1/1024+1/2048–1/4096= 0,333251953125
1/2–1/4+1/8–1/16+1/32–1/64+1/128–1/256+1/512–1/1024+1/2048–1/4096+1/8192= 0,3333740234375.
As you can see, we converge to 0.33333… or 1/3, as we carry out the calculations. If we had infinite time, we could exactly find 1/3. Even if we cannot carry out the calculations infinitely, we can employ mathematics and find that the equation is just equal to 1/3.
The answer to the question in the first part of this article can be found from equation (3).
The curious reader can answer “WHERE THE HELL IS 1/5?”.2

1 : I slightly lied here. This proof is true if the infinite sum converges to a finite number.
2 : I would like to thank Tayfun Akgül for teaching me that this article is relevant to chaos.
Translated by Bilgecan Dede
Source : Matematik ve Sonsuz (Mathematics and Infinity)
Yazar: Ali Nesin (tümünü gör)
- Where the hell is 1/3, or Introduction to Chaos - 13 December 2018

