Denklem Yazmak
Kapak görseli: Napier’in logaritma kitabı.
Matematikte günümüzde kullandığımız işaretler, neredeyse tüm milletlerin binlerce yıl boyunca katkıda bulunması sonucu olmuş. Belki de dilden bağımsız olarak bir denklemin tüm Dünya’da anlaşılmasının sebebi budur. Matematikte Babıl Kulesi yapılmaya çalışılmamış, dil tüm gezegende aynı. Eğer yarın, Yeni Dünya’yı keşfettiğimiz gibi başka bir gezegende başka bir uygarlıkla temasa geçersek, matematikteki konseptler konusunda anlaşmazlığa düşeceğimizi zannetmiyorum. Ancak bu fikirleri nasıl ifade ettiğimiz konusunda çok uyumsuzluk çekeriz.
Çok büyük sayılar için Roma sayıları kullanışlı değil, onun yerine 10’lük sisteme göre yapılmış Arap sayıları çok daha kullanışlı. Yokluğu nasıl ifade edeceğiz? Peki toplama, çıkarma, çarpma? Eşittir işareti? Bilinmeyen ‘x’ nereden geliyor? Bugün bunları tartışacağım.
Sayılar
Babılliler ilk sayı sistemini kuran insanlar. Babıllilerden önce sayı sistemi kullananlar var, ancak kayıtları pek düzenli olmadığından ya da bir işaretten ziyade taşlar, düğümler ile sayıları ifade ettiklerinden, Babıllileri ilk sayı sistemi kullanan olarak kabul edelim. Babıllilerin sayı sistemi 60’lik. Yani 1’den 60’a kadar her sayı için ayrı bir karakter var. 60’lik olmasının sebebi, 60’in bir çok sayıya bölünebilmesi. 60; 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60’a tam olarak bölünüyor.

Üstten bir çivi darbesi 1 tane, sola doğru birer çivi darbesi 10 tane oluyor temel olarak. Daha büyük bir sayı yazmak için, mesela 75, başa 1, hemen yanına 15 yazılıyor (1 x 60 + 15 = 75).
Mısırlıların hiyeroglif sistemi 10’lük. 1’den 9’a kadar yanyana çubukları çiziyorsunuz. Diğer sayılar şöyle:
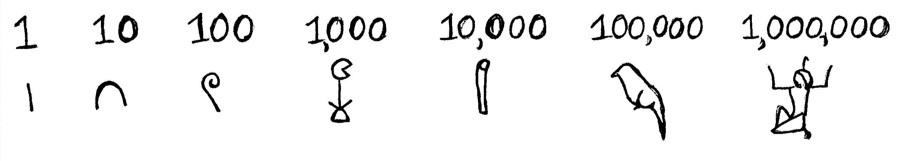
Evet, 1.000.000, “oha lan bu nasıl büyük sayı” diye ellerini açmış bir figür. 100.000 ise kurbağa yavrusu iribaş. 10 tane iribaş olunca adam niye şaşırıyor bilmiyorum. Mısırlılar, toplama için işaret kullanmışlar:  toplama,
toplama,  çıkarma anlamına geliyor.
çıkarma anlamına geliyor.
Roma sayıları, yine 10’luk. Bir kaç tane sembol var, I = 1, V = 5, X = 10, L = 50, C = 100, D = 500, M = 1000. Roma sayıları çubuğa atılan çentiklerden geliyor. 1’den 5’e kadar sayılar için birer çentik atıyorsunuz ( IIII ). Roma sayılarında çıkarma kuralı kullanılıyor. Yani, 4 yazmak için 5 – 1, IV kullanıyorsunuz. 6 için, VI. 5. çentiğe ekstra çentik atıyorsunuz ( IIIIV ya da IIIIΛ ). 10. çentiğe de ekstra bir çentik atıyorsunuz ( IIIIVIIIIX ya da IIIIΛIIIIX ).
5 tane da X olunca V’nin ortasına bir çentik atıyorsunuz: ᗐ. Zaman içinde bu sembol, N, И, K, Ψ, ⋔ ve en son Augustus zamaninda ⊥ olmuş ve kisaca L = 50 olmus.
100 için de X’e bir çentik daha atıyorsunuz, yani ?. Zaman içinde bu işaret de hızlı yazarken >I< ya da ƆIC durumuna gelmiş. Daha da kısalarak sadece Ɔ ya da C olmuş. En son C kazanmış, çünkü centum Latince’de yüz anlamına geliyor. 1000 Latince’de mille kelimesinden geliyor.
Hint sayıları (Devanagari), yine 10’luk. Şimdi kullandığımız sayı sistemi gibi. Zaten modern sayı sistemine yaklaşıyoruz. 0 १ २ ३ ४ ५ ६ ७ ८ ९. Hintliler, sıfırı ilk bulan millet. Bu sayede büyük ve ondalıklı sayıları daha kolay ifade edebiliyorlar. Sanskritce’de kullanılan ‘shunya’ ‘hiç birşey’ anlamına geliyor. Sıfır, Araplara ‘sifr'(صفر) olarak geçmiş. (Arapça bilmiyorum. O kelimeyi kopyaladım. Eğer küfür kopyaladıysam da kusura bakmayın). Millattan önce 750’li yıllardayız.
M.Ö. 5. yy.da Yunanistan’da kullanılan sayılar: ō α β γ δ ε ϝ ζ η θ ι. Bu sistemi de açıklamaya pek gerek yok, çünkü bizim sisteme benziyor. Bir ek bilgi olarak, Yunanlılar da (Batlamyus) sıfırı uzaktan keşfetmişler, ancak sıfırın anlamından ziyade, daha büyük basamaklı sayılar için yer tutucu olarak kullanmışlar.
M.S. 8.yy’da Arap yarımadası, birbirini kesen insanlardan ziyade Harezmi, Kindi, Biruni gibi muhteşem insanları çıkaran bir yer olduğundan, ileri hesaplar için iyi bir sayı sistemine ihtiyaç duyulmuş. Harezmi, Hint sayı sisteminden esinlenerek 10’luk sayı sistemini kullanmış: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Aynı yıllarda, Batı Arabistan’da başka bir sayı sistemi daha çıkmış, ٠ – ١ – ٢ – ٣ –٤ – ٥ – ٦ – ٧ – ٨ – ٩ ancak Harezmi ve Kindi’nin eserleri çok daha fazla paylaşıldığından Harezmi’nin sayı sistemi kullanılmaya devam etmiş. Harezmi’nin sayı sistemi, her bir sayıdaki açı sayısına dayanıyor. Sıfırda bir açı yok.
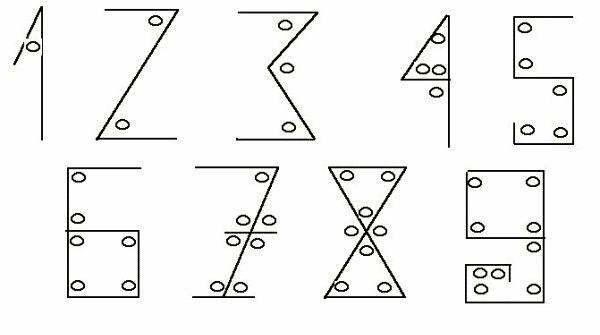
Harezmi’nin sayı sistemi Avrupa’da ilk kez, 976’da Ispanya’da dağıtılan Codex Vigilanus’ta görülmüş.

Avrupa’ya tam olarak tanıtan insan ise Fibonacci.

Şimdi 13.yy’dayız, Hintlilerin bulup, Harezmi’nin geliştirip, Fibonacci’nin “çok kullanışlı lan” diye mükemmelleştirdiği bir sistem var elimizde. Bu sistemde işlemleri bulmak lazım.
1498: Toplama + ve Çıkarma –
Artı ve eksi işareti ilk kez Johannes Widmann tarafından muhasebe işlemleri için 1498’de yazılan bir kitapta görülüyor. Latince ‘et’ (ve) kelimesinden geliyor. 5 et 7: 5 + 7 (5 ve 7).
1525: Radikal – Kök √
Avusturya’da Christoph Rudolff tarafından tanıtılıyor. ‘r’ harfinden (Latince radix) geldiği düşünülüyor. İlk halinde üstteki büyük çizgi yok. Üzerine çizgi çizmeyi ilk Descartes kullanıyor. Bundan önce radikaller, Regiomontanus tarafından sayının başına R yazarak ifade edilmiş.
1544: Parantez – Gruplama (…)
Almanya’da Michael Stifel tarafından işlemlerin öncelik sırasını göstermek için kullanılıyor.

1557: Eşittir =
Bu komik. Ingiltere’de Robert Recorde, işlem yaparken sürekli ‘is equal to’ ‘is equal to’ ‘is equal to’ diye yazmak gina getirdiğinden, ‘is equal to’ yerine sinirle kocaman iki çizgi çiziyor.
1618: Çarpma ×, Oran ∷, Artı-Eksi ±
Çarpı işaretini ilk İngiliz Matematikçi William Oughtred tanıtmış. John Napier’in logaritma cetvelini ilk kez sunduğu “Mirifici Logarithmorum Canonis Descriptio” kitabına yazdığı bir dipnotta görülmüş. St. Andrews haçından geliyor (Galler Bayrağı). Oughtred aynı zamanda, oran ∷ ve artı-eksi işaretlerini ±, sinüs için ‘sin’ ve kosinüs için ‘cos’ kullanmayı ilk kez kendi yazdığı bir kitapta tanıtmış (Recorde’nin eşittir işareti 50 yılda yayılmış ashahashfahsdgl).


1631: Küçük Büyük İşaretleri < >
İngiliz Thomas Harriot tarafından, Artis Analyticae Praxis ad Aequationes Algebraicas Resolvendas (The Analytical Arts Applied to Solving Algebraic Equations) kitabında görülmüş. Harriot, Amerika yerlilerine büyük ilgi duymuş ve bu konuda da çalışmalar yapmış. Büyük küçük işaretinin, Harriot’un Amerika gezisi sırasında bir yerlide gördüğü 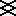 dövmesinden geldiği söyleniyor. Daha sonra Leonhard Euler tarafından büyük değildir, küçük değildir işaretlerinin kullanımı burada:
dövmesinden geldiği söyleniyor. Daha sonra Leonhard Euler tarafından büyük değildir, küçük değildir işaretlerinin kullanımı burada:

1634: Paralel ∥, Dik ⊥
Pierre Herigone tarafindan yazılan Cursus mathematıcus kitabında tanıtılmış.

1637: Üstel xy
Rene Descartes’in Geometri kitabında görülmüş. ‘aa çarpmasını kısa yazmak için a2 kullanacağım’ demiş.

Bundan önce, bir sayının sekizinci kuvvetini göstermek için Robert Recorde, zenzizenzizenzic kelimesini önermiş. Zenzic : Almanca’da karesini almak.

1637: Bilinmeyen, x, y, z
Rene Descartes tarafından La Geometrie’de Arapca’daki şey kelimesinden kullanılmış.

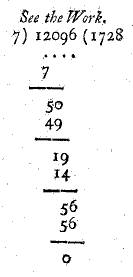
1659: Bölme ÷, ‘Böylece’ ∴
Isvicre’li matematikçi Johann Rahn tarafından kullanılmış.

Okullarda kullanılan bölme sistemi ilk kez Amerika’da 1772’de bir kitapta görülmüş.
1655: Sonsuz ∞
John Wallis tarafından De sectionibus conicis (On Conic Sections)’da kullanılmış. Wallis nereden bulduğu konusunda çok fazla spekülasyon var. Kimi latince küçük omega, Hristiyanlik’ta 8 sayısının önemli olması, Roma’da kendini kuyruğundan yiyen yılandan geldiği konusunda tartışmalar var. Ama, sembol çok şık sembol şimdi, doğruya doğru. Aynı zamanda Willis, infinitezimal için 1/∞ kullanmış.

1675: Diferansiyel d, Integral ∫
dy/dx notasyonu, Gottfried Leibniz tarafından yazılan, türevin de ilk kez tanıtıldığı 11 Kasım 1675 tarihli makalede çıkıyor. Birinci türev (f’), ikinci türev (f”) notasyonu Lagrange tarafından, 1797 tarihli Théorie des fonctions analytiques kitabında kullanılıyor.

Integral ise Leibniz tarafından summa yerine, uzun S olarak kullanılıyor.
1755: Toplam Σ
İlk kez Leonhard Euler tarafından Institutiones Calculi Differentialis (Foundations of Differential Calculus) kitabında kullanılmış.

1846: Gradiyent ∇
William Rowan Hamilton tarafından An Elementary Treatise on Quaternions kitabında yan yatmış şekilde kullanılıyor.
![]()
1855: Matris
Arthur Cayley, determinanti hesaplamak için matris notasyonunu kullanmış. Ancak, terimler arasına virgül koyarak kullanmış.

1903: Skaler Çarpım ·, Vektör Çarpım ×
J. W. Gibbs’in Elements of Vector Analysis Arranged for the Use of Students in Physics kitabında ilk kez geçmiş.

1909: Büyük-O O(…), küçük-o o(…) notasyonu
Edmund Landau tarafından, Handbuch der Lehre von der Verteilung der Primzahlen kitabında ilk kez geçmiş.

Yazar: Bilgecan Dede
Bilgecan Dede
Yazar: Bilgecan Dede (tümünü gör)
- Fourier Serisi yazısına ek: - 23 Aralık 2018
- Yapay zekâ yüzünden kaybolacak ve eklenecek iş sayıları, bir tabloda - 4 Nisan 2018
- 130 yıl sonra gelen adalet: Telefonun mucidi resmî olarak Antonio Meucci! - 18 Şubat 2018
- Denklem Yazmak - 6 Ocak 2018
- Temel Harmonikler ve Lissajous Eğrileri - 17 Aralık 2017




